幻立方

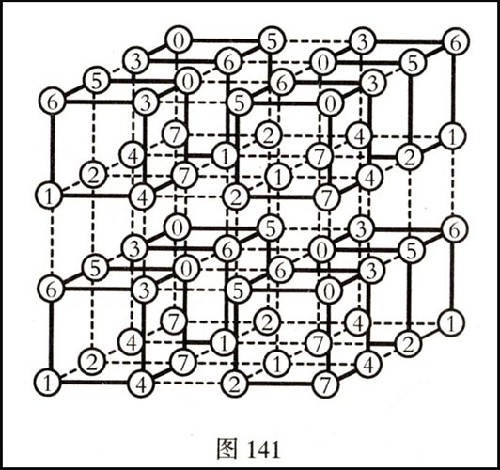
N階幻立方是n³個不同整數形成的數陣，任意行列組和對角線上的數字和都相等，這個和稱為“幻和”。如果數字是前n³個正整數，則稱其為正規的。此時幻和等於n(n³+1)/2,而且以3n²+4種形式出現。

基本介紹

• 中文名：幻立方
• 外文名：Magic cube
• 領域：數學
• 類型：複雜

簡介

幻立方是幻方向三維空間的自然延伸，而立方體是我們非常熟悉的形象，最為常見的空間圖形；這就便於我們對之研究，從中得到新穎的知識。

幻立方是由自然數1到n組成邊長為n的正方體。由上向下（k軸）是從第一層到第n層，每一層均是n行×n列的一個正方形，我們稱之為一個直剖面。同理，立方體還有另兩個方向的直剖面：從後向前（i軸）方向的面，從左到右（j軸）方向的片。由n個元素（數字）組成的直線(段)有橫向（平行於j軸）的行、縱向（平行於i軸）的列、垂直方向（平行於k軸）的稱豎或柱各n²條，總計是3n²條。n階立方體有四條(體)對角線，三個方向共6n條剖面對角線。

圖1

等級分檔

（1）當n階立方體的所有即3n條直線上的n數之和滿足於幻和S=(n+1)n/2，如此是基本的必要條件，稱之為n階立方陣；同時它的四條（體）對角線也滿足於幻和，我們稱這立方體是一個n階簡單幻立方。

（2）當一個n階簡單幻立方又有6n條剖面對角線滿足於幻和，即這3n個直剖面均為（廣義）幻方，此時稱其為n階標準幻立方。

（3）當一個n階立方體中的所有的直線、二維斜線、三維斜線上，n數之和都滿足於幻和，則這個數字立方體稱為完美幻立方。

實例

四階幻立方實例

第一層

1	8	61	60
62	59	2	7
52	53	16	9
15	10	51	54

第二層

48	41	20	21
19	22	47	42
29	28	33	40
34	39	30	27

第三層

49	56	13	12
14	11	50	55
4	5	64	57
63	58	3	6

第四層

32	25	36	37
35	38	31	26
45	44	17	24
18	23	46	43

五階標準幻立方實例：

國外已有高手作出五階標準幻立方，特地摘錄如下，給愛好者觀賞、學習。

這是幻立方的第 1 層：

67	18	119	106	5
116	17	14	73	95
40	50	81	65	79
56	120	55	49	35
36	110	46	22	101

這是幻立方的第 2 層：

66	72	27	102	48
26	39	92	44	114
32	93	88	83	19
113	57	9	62	74
78	54	99	24	60

這是幻立方的第 3 層：

42	111	85	2	75
30	118	21	123	23
89	68	63	58	37
103	3	105	8	96
51	15	41	124	84

這是幻立方的第 4 層：

115	98	4	1	97
52	64	117	69	13
107	43	38	33	94
12	82	34	87	100
29	28	122	125	11

這是幻立方的第 5 層：

25	16	80	104	90
91	77	71	6	70
47	61	45	76	86
31	53	112	109	10
121	108	7	20	59

5階立方體的幻和為：315，一共檢驗了75+4線上5數之和：D是一個簡單幻立方。

又檢驗了30條直剖面上兩對角線上n數之和：D是一個標準幻立方。