七階幻立方的數量也很巨大,應該使用編號將它們加以區別。下面的七階幻立方的編號是:15-35-51-552系列1234567。
基本介紹
- 中文名:七階幻立方
- 所屬類型:科學
- 所屬類別:數學
- 所屬科目:幾何
簡介,事件,事發經過,7階幻立方解法,
簡介
在平面幻方中,可以通過加框法得到任意大於等於5階的同心幻方,推廣到幻立方,當階數等於偶數時,由於大小數可以在任意一個平面中進行均勻搭配,所以可以輕鬆的進行無限的遞推加框,當階數為奇數時,任意一個平面中的數據個數為奇數個,無法進行均勻搭配,很難加框,經過長期探索才找到一些特殊的方法來加框。
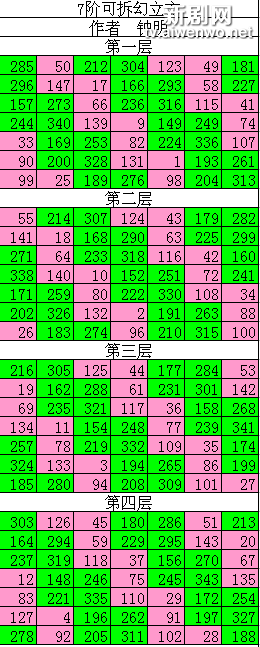
15-35-51-552的意思是:它是使用15號七階和方做左位數,35號七階和方做中位數,51號七階和方做右位數,第一層左上角的數是七數制的552(換成十進制是226)。
第一至第七層左上角的七數制數依次是:552、166、473、717、324、631、245。換成十進制數依次是:226、41、192、301、109、260、75。
這個幻立方的整體也是中心對稱的。
主視圖第一層
226 252 320 4564139 158
115 183 209 277 296 2896
472147 166 234 253 328
285 304 2955123 191 217
174 242 261 336 128099
63131 150 218 293 312 37
337 2088107 182 201 269
主視圖第二層
4160128 154 222 290 309
273 341 1785111 179 198
155 230 249 317 4968136
93119 187 206 274 300 25
325 176144 163 238 257
214 282 308 3352120 195
103 171 239 265 333 984
主視圖第三層
192 211 286 305 3056124
81100 175 243 262 330 13
313 3857132 151 219 294
202 270 338 2189108 176
140 159 227 246 321 4665
2297116 184 210 278 297
254 329 573141 167 235
主視圖第四層
301 2694113 188 207 275
232 258 326 277145 164
121 196 215 283 302 3453
1078104 172 240 266 334
291 310 4261129 148 223
180 199 267 342 1886112
69137 156 231 250 318 43
主視圖第五層
109 177 203 271 339 1590
4766134 160 228 247 322
279 298 2398117 185 204
168 236 255 323 674142
50125 193 212 287 306 31
331 1482101 169 244 263
220 288 314 3958133 152
主視圖第六層
260 335 1179105 173 241
149 224 292 311 3662130
87106 181 200 268 343 19
319 4470138 157 225 251
208 276 295 2795114 189
146 165 233 259 327 371
3554122 190 216 284 303
主視圖第七層
75143 162 237 256 324 7
307 3251126 194 213 281
245 264 332 883102 170
127 153 221 289 315 4059
1691110 178 197 272 340
248 316 4867135 161 229
186 205 280 299 2492118
事件
第二季《最強大腦》節目中,七階幻立方挑戰者陳大紀不服評判,現場“約架”,叫板中國幻方協會的權威專家,獨孤求敗兩年的他力邀專家現場PK,火藥味十足的爭辯從節目一路演化成微博口水戰,幻方協會主席的表態更是讓這場論戰撲朔迷離。DR魏的打分是否合理,幻立方的難度究竟如何評判,網友爭相圍觀、紛紛表態!
事發經過
現場挑戰完美七階幻立方的陳大紀在完成挑戰後,節目組邀請來了中國幻方協會的副主席曾學涵進行驗證。當被問起完成七階幻立方能夠有多少人時,曾副主席表示:“我們協會的現有的主席團都有可以!”主持人又發問,這當中能完成151階的能有多少人,曾副主席自信地說:“可能在一個手掌吧。”不料曾先生的這兩個回答“惹惱”了挑戰者陳大紀。
作為幻立方世界記錄保持者,陳大紀一直在強調“這不可能!”因為並不是每個點都有解的,他堅信這項挑戰的難度。陳大紀力邀曾副主席現場對決,並表示“已經獨孤求敗兩年了!我們現場比賽,看誰算的更快!”曾先生則表示自己並非是協會中能力最強的,不能代表整個協會。二人舌戰正酣,最終孟非給了雙方一個台階下,兩人約定好私下裡進行挑戰。
7階幻立方解法
《我的小小自白》節目播出後,網路上對我的負面評價不少,概括起來支持選手主要原因有三點:第一,他是民間科學達人,我本人反成了科學“高官”。【事實的真相是:陳大紀是中央黨校畢業,百分百的中國公務員,典型官僚;我們協會是一個自發的鬆散的民間的幻方研究協會,我掛著協會副主席的虛名,沒有一分錢的工資,還倒貼時間與金錢,是千千萬萬漂泊務工的屌絲一枚。】第二:他是世界紀錄保持者,這是他自吹自擂、糊弄人的光環。【事實真相是:世界上根本不存在什麼最高階的幻方、幻立方,這簡直就是一個國際笑話。以下是一個大於7的質數P階完美幻立方公式:A(i,j,k)=(i+2j+4k)*P*P+ (2i+4k+j)*P+(4i+j+2k)mod(P)。所謂最高階——還特別說什麼151階,這種所謂記錄,只是一個無知無畏的國際笑話。
佟大為選定的初始位置在選手視角調整之後,為A (a,b,c)= (6,6,3),也就是在第6層第6行第3列中放置起始數字1。
這一7階標準幻立方中的參數:
1、初始位置A(k0,i0,j0)= A (a-1,b-1,c-1)= (5,5,2)=1
2、連續向量 (k1,i1,j1)=(0,-1,3),也即連同起始位,連續放7個數字。
3、小轉向量(k2,i2,j2)=(1,-2,1),也就是遇到7的倍數,但不是49的倍數時轉向
4、大轉向量(k3,i3,j3)=(-3,4,-2),也就是遇到49的倍數時轉向
與平面相比,幻立方多了一個大轉向向量。我告訴大家一點,大轉向向量是不用記的——選手未必知道這一點,因為他基本上是靠交換變換出來然後死記硬背的,根本不懂背後的深刻的原理與規律,否則如果懂得,既不會花幾個月去折騰,更不會自大狂妄到認定全世界只有他能他會,這種種跡象表明,他對於這一方法的深刻的原理是不知的,最多只是知其然而不知其所以然。
我已經論證到,假設初始位置為A(k0,i0,j0)(這是在(0,P-1)表示系統中),則當大轉向向量為(k3,i3,j3)= (2*k0+1,2*i0+1,2*j0+1)mod(P)時,必定可以生成中心對稱的效果,這一條件是充要條件。舉上一例而言,由於 A(k0,i0,j0)= (5,5,2),則若要中心對稱,則必有(k3,i3,j3)= (2*5+1,2*5+1,2*2+1)mod(7)=(11,11,5)mod(7)=(4,4,5)mod(7),請注意,在實際構造效果中, (4,4,5)mod(7)與(-3,4,-2)mod(7)是完全等價的。
走步的方法跟17、18世紀即已知的平面的連續擺數法是一模一樣的。為了照顧普通大眾,我們舉幾個例子進行說明。
在(0,P-1)表示系統中,
由於A(k0,i0,j0)= A (a-1,b-1,c-1)= (5,5,2)=1,它表示的意思是在第6層第6行第3列中放置起始數字1。按照連續向量(k1,i1,j1)=(0,-1,3),則下一個位置為 A(5,5,2)+(0,-1,3)=A(5,4,5)=2,也即第6層第5行第6列中放置數字2;繼續按照連續向量,則下一個位置為A(5,4,5)+ (0,-1,3)=A(5,3,8)= A(5,3,1)=3,也即第6層第4行第2列中放置數字3;以此類推,可得A(5,6,6)= 7,也即第6層第7行第7列中放置數字7。
這個時候,出現了第一個7的倍數,但不是49的倍數,這就需要按照小轉向向量來處理。按照小轉向向量(k2,i2,j2)=(1,-2,1),下一個位置為A(5,6,6)+(1,-2,1)=A(6,4,7)=A(6,4,0)=8,也即第7層第5行第1列中放置數字8;然後又以此為初始,繼續按照連續向量(k1,i1,j1)=(0,-1,3)進行放數。以此類推,一直到A(4,0,1)= 49,也即第5層第1行第2列中放置數字49。
這個時候,出現了第一個49的倍數,這就需要按照大轉向向量來處理。按照大轉向向量(k3,i3,j3)=(-3,4,-2),下一個位置為 A(4,0,1)+(-3,4,-2)=A(1,4,-1)=A(1,4,6)=50,也即第2層第5行第7列中放置數字50,然後又以此為初始,繼續按照連續向量(k1,i1,j1)=(0,-1,3)進行放數。
根據上述過程,不斷重複進行,即可逐一填出7階標準幻立方來。上述過程的核心,就是四組向量參數:
1、初始位置A(k0,i0,j0)= A (a-1,b-1,c-1)= (5,5,2)=1
2、連續向量 (k1,i1,j1)=(0,-1,3),也即連同起始位,連續放7個數字。
3、小轉向量(k2,i2,j2)=(1,-2,1),也就是遇到7的倍數,但不是49的倍數時轉向
4、大轉向量(k3,i3,j3)=(-3,4,-2),也就是遇到49的倍數時轉向
任何一個人,記住這四組參數,按照連續走步的規則,就可以把這個7階標準幻立方“填寫”出來。這就是我們為什麼有信心說,可以教會小學生對陳姓選手進行 PK,原因就是這么簡單,每一個位置——342個位置,只要記4組參數即可,根據中心對稱的原理,實際上只需記3組參數即可,大轉向向量可以根據初始位置直接給出。理論上,全部的記憶量為342*3*3=3078個數字。
另外,如果考慮到幻立方視角的旋轉、反射等角度,實際上並不需要記那么多,也就是不考慮任何保性變換,而只考慮視角的轉換,那么理論上的總的記憶量為3078/24=128.25,也就是不超過130個需要記憶,由於每組9個數字,則128.25/9=14.25,據李文老師測算,不考慮任何保性變換,實際總共需要記憶19套參數,也即19*9=171個數字即可通過視角轉換到事先準備好的參數,今後一一進行走步即可。
這一7階標準幻立方中的參數:
1、初始位置A(k0,i0,j0)= A (a-1,b-1,c-1)= (5,5,2)=1
2、連續向量 (k1,i1,j1)=(0,-1,3),也即連同起始位,連續放7個數字。
3、小轉向量(k2,i2,j2)=(1,-2,1),也就是遇到7的倍數,但不是49的倍數時轉向
4、大轉向量(k3,i3,j3)=(-3,4,-2),也就是遇到49的倍數時轉向
與平面相比,幻立方多了一個大轉向向量。我告訴大家一點,大轉向向量是不用記的——選手未必知道這一點,因為他基本上是靠交換變換出來然後死記硬背的,根本不懂背後的深刻的原理與規律,否則如果懂得,既不會花幾個月去折騰,更不會自大狂妄到認定全世界只有他能他會,這種種跡象表明,他對於這一方法的深刻的原理是不知的,最多只是知其然而不知其所以然。
我已經論證到,假設初始位置為A(k0,i0,j0)(這是在(0,P-1)表示系統中),則當大轉向向量為(k3,i3,j3)= (2*k0+1,2*i0+1,2*j0+1)mod(P)時,必定可以生成中心對稱的效果,這一條件是充要條件。舉上一例而言,由於 A(k0,i0,j0)= (5,5,2),則若要中心對稱,則必有(k3,i3,j3)= (2*5+1,2*5+1,2*2+1)mod(7)=(11,11,5)mod(7)=(4,4,5)mod(7),請注意,在實際構造效果中, (4,4,5)mod(7)與(-3,4,-2)mod(7)是完全等價的。
走步的方法跟17、18世紀即已知的平面的連續擺數法是一模一樣的。為了照顧普通大眾,我們舉幾個例子進行說明。
在(0,P-1)表示系統中,
由於A(k0,i0,j0)= A (a-1,b-1,c-1)= (5,5,2)=1,它表示的意思是在第6層第6行第3列中放置起始數字1。按照連續向量(k1,i1,j1)=(0,-1,3),則下一個位置為 A(5,5,2)+(0,-1,3)=A(5,4,5)=2,也即第6層第5行第6列中放置數字2;繼續按照連續向量,則下一個位置為A(5,4,5)+ (0,-1,3)=A(5,3,8)= A(5,3,1)=3,也即第6層第4行第2列中放置數字3;以此類推,可得A(5,6,6)= 7,也即第6層第7行第7列中放置數字7。
這個時候,出現了第一個7的倍數,但不是49的倍數,這就需要按照小轉向向量來處理。按照小轉向向量(k2,i2,j2)=(1,-2,1),下一個位置為A(5,6,6)+(1,-2,1)=A(6,4,7)=A(6,4,0)=8,也即第7層第5行第1列中放置數字8;然後又以此為初始,繼續按照連續向量(k1,i1,j1)=(0,-1,3)進行放數。以此類推,一直到A(4,0,1)= 49,也即第5層第1行第2列中放置數字49。
這個時候,出現了第一個49的倍數,這就需要按照大轉向向量來處理。按照大轉向向量(k3,i3,j3)=(-3,4,-2),下一個位置為 A(4,0,1)+(-3,4,-2)=A(1,4,-1)=A(1,4,6)=50,也即第2層第5行第7列中放置數字50,然後又以此為初始,繼續按照連續向量(k1,i1,j1)=(0,-1,3)進行放數。
根據上述過程,不斷重複進行,即可逐一填出7階標準幻立方來。上述過程的核心,就是四組向量參數:
1、初始位置A(k0,i0,j0)= A (a-1,b-1,c-1)= (5,5,2)=1
2、連續向量 (k1,i1,j1)=(0,-1,3),也即連同起始位,連續放7個數字。
3、小轉向量(k2,i2,j2)=(1,-2,1),也就是遇到7的倍數,但不是49的倍數時轉向
4、大轉向量(k3,i3,j3)=(-3,4,-2),也就是遇到49的倍數時轉向
任何一個人,記住這四組參數,按照連續走步的規則,就可以把這個7階標準幻立方“填寫”出來。這就是我們為什麼有信心說,可以教會小學生對陳姓選手進行 PK,原因就是這么簡單,每一個位置——342個位置,只要記4組參數即可,根據中心對稱的原理,實際上只需記3組參數即可,大轉向向量可以根據初始位置直接給出。理論上,全部的記憶量為342*3*3=3078個數字。
另外,如果考慮到幻立方視角的旋轉、反射等角度,實際上並不需要記那么多,也就是不考慮任何保性變換,而只考慮視角的轉換,那么理論上的總的記憶量為3078/24=128.25,也就是不超過130個需要記憶,由於每組9個數字,則128.25/9=14.25,據李文老師測算,不考慮任何保性變換,實際總共需要記憶19套參數,也即19*9=171個數字即可通過視角轉換到事先準備好的參數,今後一一進行走步即可。

