基本介紹
- 中文名:平面連桿機構
- 外文名:Planar linkage
- 性質:一種傳動裝置結構
- 分類:四桿機構和多桿機構
特點
分類
基本類型
雙曲柄機構
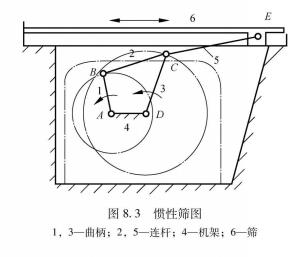
曲柄搖桿機構

雙搖桿機構

曲柄存在條件
平面四桿機構簡介
 平面連桿機構
平面連桿機構



 平面連桿機構
平面連桿機構平面連桿機構是由若干構件用低副(轉動副、移動副)連線組成的平面機構。最簡單的平面連桿機構由四個構件組成,稱為平面四桿機構。平面連桿機構廣泛套用於各種機械、...
連桿機構(Linkage Mechanism)又稱低副機構,是機械的組成部分中的一類,指由若干(兩個以上)有確定相對運動的構件用低副(轉動副或移動副)聯接組成的機構。平面連桿...
基本信息現代連桿機構設計 作者:熊濱生 主編 出版日期:2006年2月 書號:7-5025-8057-3 開本:32 裝幀:平 版次:1版1次 頁數:248頁內容簡介本書闡述了連桿機構...
《平面機構綜合》由若干個剛性構件通過低副(轉動副、移動副)聯接,且各構件上各點的運動平面均相互平行的機構,又稱平面低副機構。低副具有壓強小、磨損輕、易於...
《連桿機構的分析與綜合》是2002年科學出版社出版的圖書,作者是曹惟慶。...... 本書是《平面連桿機構分析與綜合》(科學出版社,1989)一書的第二版。本書第一章介...
《平面連桿機構的過約束及自調結構的分析與設計研究》是2003年由安培文所著的博士論文。...
曲柄連桿機構是指用曲柄和滑塊來實現轉動和移動相互轉換的平面連桿機構。曲柄滑塊機構中與機架構成移動副的構件為滑塊,通過轉動副聯接曲柄和滑塊的構件為連桿。...
構件呈平行四邊形的平面連桿機構。它是一種鉸鏈四桿機構﹐根據曲柄存在條件屬於雙曲柄機構(見圖 平行四邊形機構 )。...
機械原理:曲柄滑塊機構,用曲柄和滑塊來實現轉動和移動相互轉換的平面連桿機構﹐也稱曲柄連桿機構。...
《基於MATLAB/Simulink平面連桿機構的動態仿真》是2007年哈爾濱工業大學出版社出版的圖書。...
本書結合機械設計的知識和方法,分析了機構的設計要點。圖解的機構主要包括平面連桿機構、凸輪機構、齒輪機構、間歇運動機構、組合機構等常用機構。本書內容全面,講解...
本書精選了約380個機構實例,囊括了平面連桿機構、凸輪機構、齒輪機構、輪系、間歇運動機構、螺旋機構、撓性傳動機構、組合機構、特殊機構以及創新機構等全部的機構類型...
機構,指由兩個或兩個以上構件通過活動聯接形成的構件系統。按組成的各構件間相對運動的不同,機構可分為平面機構(如平面連桿機構、圓柱齒輪機構等)和空間機構(如...
從Ft=Fcosα知,當壓力角α=90°時,對從動件的作用力或力矩為零,此時連桿不能驅動從動件工作。機構處在這種位置成為死點,又稱止點。死點就是處於直線位置上。...
第五節 平面四桿機構的設計 第六節 平面五連桿機構 學習指導1.3 思考題1.3 習題1.3 第四章 凸輪機構及其設計 第一節 凸輪機構套用及分類 第二節 從動件...
全書共分十六章.主要介紹:平面機構運動簡圖及自由度;平面連桿機構;凸輪機構;步進運動機構;鍵、銷聯接;螺紋聯接與螺旋傳動;帶傳動;鏈傳動;齒輪傳動;蝸桿傳動;軸;軸...
本書共分12章, 主要內容有: 緒論、機構的結構分析、平面連桿機構、凸輪機構、齒輪機構、輪系、間歇運動機構和其它常用機構、機械系統動力學、機械的平衡、機械執行...
