平行板電容器

平行板電容器

平行板電容器是在兩個相距很近的平行金屬板中間夾上一層絕緣物質——電介質（空氣也是一種電介質）組成的一個最簡單的電容器。平行電容器是由兩塊彼此平行放置的金屬板所構成的。

平行板電容器是最簡單的，也是最基本的電容器，幾乎所有電容器都是平行板電容器的變形。

基本介紹

  • 中文名：平行板電容器
  • 外文名：plane-parallel capacitor
  • 帶電特點：兩板帶等量異號電荷
  • 電容量：與面積和板間距有關
  • 公式：C=εS/4πkd
  • 套用學科：物理學
基本信息,勻強電場,電容公式,電場強度,公式,

基本信息

圖為1個平行板電容器及其外形尺寸，每個極板的面積為A（實際上A為每個單極板的面積）。如果矩形極板的寬度為W，長度為L，則其面積為A=W×L。該電容器的極板是平行的，其間距為d。
電容器外形電容器外形
如果兩極板的間距d遠小於它們的寬度和長度，則該電容器的電容近似為 C=εA/d
其中，ε為兩極板間材料的介電常數。對於真空介質，其介電常數為ε=ε0=≈8.85×10-12F/m
那么對於其他物質，介電常數為ε=ε0εr
其中，εr為相對介電常數。下表給出了幾種物質的相對介電常數大小。
幾種物質的相對介電常數
物質
相對介電常數（F/m）
物質
相對介電常數（F/m）
空氣
1.0
石英
4.3
鑽石
5.5
二氧化矽
3.9
雲母
7.0
水
78.5
聚酯
3.4

勻強電場

1．電壓U一定的情況
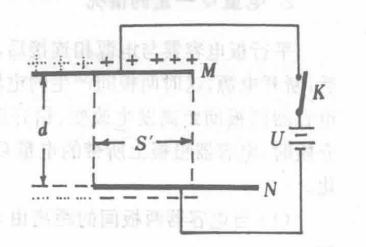
如圖12—1所示，平行板電容器C與一電源連線，兩板間距離為d，當開關k閉合穩定後，電容器兩板間電壓為U，這時兩板間產生的電場強度為E=U/d ①
平行板電容器平行板電容器
此後，無論其它條件如何變化，且開關始終閉合時，電容器M、N兩極板間的電壓U始終不變，即U一定。
（1）當將兩極板間的距離由d增大到dˊ時。由①式可知，這時兩板問的電場強度變為Eˊ=U/dˊ，即電場強度減小。為什麼電場強度會減小呢?其實這與兩極板上所帶的電量有關。平行板電容器間所產生的電場強度（當兩板間無介質時），由極板上電量的面電荷密度來決定，面電荷密度越大，其間產生的電場越強。在兩板間距離d增大時，電容器的容量C減小，由θ=U·C知，極板上所帶電量減小，在面積S一定時，其面電荷密度減小，故場強減小。
（2）如果保持兩板間距離d不變，而使兩板的面積錯開，這時電容器的正對面積由原來的S減小為Sˊ，如圖所示。電容器的電容C減小，極板上所帶電量減小，這時似乎兩板間的電場強度E也要減小，其實不然。在電量Q減小時，這些較少的電量全部分布在較小的正對面積Sˊ上，而Sˊ之外的錯開部分極板上這時無電荷。因面積減小，較小面積上所帶的總電量較前也有所減
少，而電荷的面密度分布卻保持未變（證明從略），則其間的電場強度保持不變。由①式也清楚地反映了這一點。故在電壓一定的條件下，改變電容器的正對面積，不改變其間所產生的電場強度大小，而只改變電容器極板上所帶的絕對電量的多少．面積越小，極板上所帶的絕對電量越少。
平行板電容器平行板電容器
（3）若保持電容器兩板間距離d和正對面積S不變，而在其間加入介電常數為￡的電介質時，電容器的電容量增大，兩板所帶電量也隨之增大，但這時電介質在靠近電容器極板兩側分別感應出少量與該極板上所帶電荷電性相反的感應電荷，感應電荷產生的電場與原電荷在極板間產生的電場方向相反，疊加的結果並不能使電場強度增加，而仍保持不變。①式正反映了這一性質。可見，在電壓U一定的條件下，電容器兩極板間加入介質，而其間的電場強度保持不變。
2．電量Q一定的情況
平行板電容器與電源相連線後，兩極板被電源充電，穩定後，斷開電源，這時兩板間產生的電場強度仍由①式決定。當電容器兩板間距離發生改變、錯開正對面積或兩板間加入電介質時，電容器極板上所帶的電量Q=UC一定，並不發生變化。
當電容器兩板間的距離由d增大到dˊ時，由Cα1/d知
Cˊ/C = d/dˊ ②
因電容器帶電量一定，由Q=UC知，Uα1/c，則
Uˊ/U = C/Cˊ③
由②、③兩式可知
Uˊ/U= dˊ/d ④
即 Uˊ/dˊ=U/d ⑤
⑤式說明，電容器電量一定時．改變兩極板間的電壓，則變化後兩板問的電壓與兩板間距離之比與改變前的比值相等，保持不變。由①式可知，這時兩板間產生的電場強度也保持不變。這一點是容易理解的，因兩板間距離改變之後，極板上電量保持不變，在兩極板相對面積S一定的條件下，極板上的面電荷密度保持不變，故電場強度保持不變。

電容公式

平行板電容器的電容量是隨兩板的相對面積和兩板間的距離的變化而變化的。並且與兩板間的電介質有關。那么，平行板電容器的電容量，與兩板的相對面積和板間距離，以及兩板間的電介質有何關係呢?實驗證明，平行板電容器的電容量是與兩板的相對面積S成正比；與兩板間的距離d成反比；與兩板間電介質的介電常數ε成正比的。把這種關係寫成等式。即
C =εS/d= ε0*εrS/d =εrS/4πkd
式中的ε0是比例常數，它在數值上等於兩板間是真空對，兩個單位面積的平行金屬板相距一個單位距離時，這個電容器的電容量。它的具體數值是隨選用的單位不同而不同的。當相對面積的單位用m2，距離的單位用m，電容量的單位用法拉時，則ε0 = 1/4πk =8.85×10-12法拉/米，ε0又叫做絕對介電常數。式中εr是平行板間的電介質的介電常數，又叫做相對介電常數。

電場強度

設平行板A、B各帶面電荷密度分別為+σ和-σ，板間的介電常數為ε0εr，距離為d。EA和EB分別為帶電A板和帶電B板的電場強度如圖所示。
帶電平行板帶電平行板
（1）兩板的外側 EA + EB =0
（2）兩極間 EA + EB =E， EA= EB =σ/ε0εr，E =2σ/2ε0εr=σ/ε0εr
上式則為兩個無限大帶異性電荷平板之間的電場強度。

公式

理論分析表明，當平行板電容器的兩極板間充滿同一種介質時，電容C與極板的正對面積S、極板距離d的關係為
若平行板電容器的兩極板間是真空時，則公式中沒有相對介電常數ε（relative dielectric constant )，由公式可知，電容C與ε、S成正比（即ε、S越大，C越大）；與d成反比d越大，C越小）。
若兩極板間為勻強電場，電場強度記作E, 則有：
1. U =Ed
2. Q= UC （其中Q為電容器所帶電荷量，U為兩極板間電壓）

相關詞條

熱門詞條

聯絡我們