帕里斯結果(result of Paris)關於自然數的一個命題.它是真的,但在佩亞諾算術中不能證明.它也是此方面的第一個例子.首先由帕里斯(Paris ,J.)和柯比(Kirby, L.)證明,後來哈林頓(Harring-ton,L.)發現這是有限拉姆齊定理的一個簡單擴充.該定理是證明論中近年來最重要的成果,引起人們的注意.
設H是自然數集的一個有限子集,如果H所含自然數的個數Card (H)}min(H),就說H是相對大的.給定自然數e,r,k和集合M,令
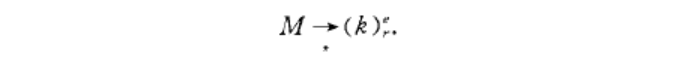
上式表示對每一個分割P : [M]`}r,存在自然數集的一個相對大的有限子集HcM,使得P對H是齊次的,並且H至少含有k個自然數,其中[M]一{FcM} }F}-e},如果P在[H]‘上是一個常數,則稱P相對於H是齊次的.
1.對所有自然數。,r,k,存在一個集合M使得M} (k );.該結果的證明用到無限拉姆齊定理,可表示為佩亞諾算術中的一個命題.
2.由結果1確定的組合原則在佩亞諾算術中不可證明.
