基本介紹
- 中文名:布蘭德規則
- 外文名:Bland rule
- 所屬學科:數學
- 所屬問題:線性規劃
- 提出者:布蘭德(R.G.Bland)
基本介紹


相關介紹















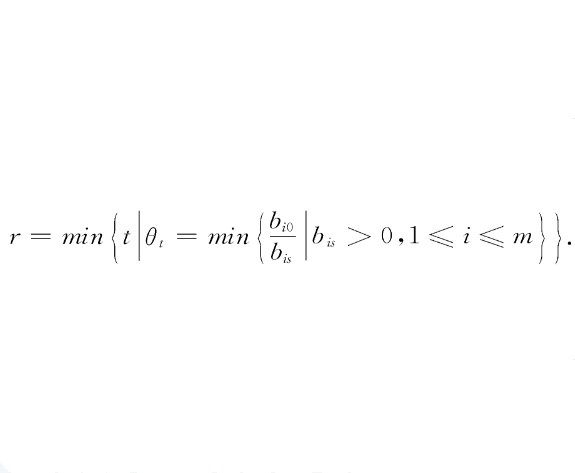

















布蘭德規則(Bland rule)是一種用單純形法求解線性規劃問題時避免循環的方法,它是布蘭德(R.G.Bland)於1977年提出的,此方法比字典序法簡單得多,在國際上受到很多人的重視,認為是線性規劃中一項很好的成果,...
布蘭德桉(學名:Eucalyptus brandiana Hopper & McQuoid)是桃金孃科、桉屬植物。樹高達5米。不存在一個木質塊莖。樹冠局限於樹枝的上部。樹皮光滑,呈灰色至銀灰色和鮭魚色,呈不規則條狀脫落。成葉粗、厚,通常互生,葉柄長3.8-4...
布蘭德 布蘭德,是一名德國職業足球教練。現在執教德國足球甲級聯賽的不萊梅足球俱樂部。
斯圖爾特·布蘭德是一個顛覆常理的人,而《地球的法則:21世紀地球宣言》則再次顯示出他思維的高度,也是他一生當中最重要的一本書。正如《地球的法則:21世紀地球宣言》標題所暗示的,這本書講的是如何進行有規則的思考。這本書有科學家...
按照慣例,NBA選秀抽籤儀式規則如下:將14個分別標有數字1到14的桌球放入一個鼓狀的圓桶中,從它們中任取4個球構成一種組合結果,一共將有1001種組合結果。如果將其中一種結果忽略不計的話,剩餘1000種結果將由電腦隨機分配給13支...
模式規則 歡迎來到(雙人)野區 極限閃擊是個快節奏(約15分鐘)的實驗性模式,專為追求以新鮮的方式與低壓力樂趣遊玩英雄聯盟的你而設計。比起緊張的比賽,它強化了刺激和驚喜的部分,並且依舊會對你從英雄聯盟其他模式中學習到的技巧...
第5節 背離有效的法律規則 41 第6節 偏離的裁量權 43 第7節 法律原則 44 第8節 未經法律授權偏離法律 46 第9節 裁量權vs.偏離 47 第10節 未經法律授權的偏離類型 49 第11節 偏離與“司法能動主義” 51 第12節 法官的精神...
