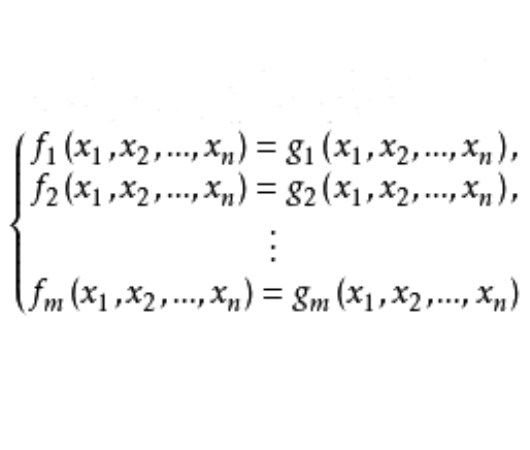布爾方程組

布爾方程組(system of Boolean equations)是布爾方程構成的方程組，在布爾代數B中，由2m個n元布爾函式(可分為兩組)f_i(x₁，x₂，…，x_n)，g_i(x₁，x₂，…，x_n)，(i=1，2…，m)可組成m個布爾方程，f_i(x₁，x₂，…，x_n)=g_i(x₁，x₂，…，x_n)，(i=1，2，…，m)，這m個方程所構成的方程組稱為B上的布爾方程組。

基本介紹

• 中文名：布爾方程組
• 外文名：system of Boolean equations
• 所屬學科：數學（布爾代數）
• 簡介：布爾方程構成的方程組

基本概念

在布爾代數B中，由2m個n元布爾函式(可分為兩組)f_i(x₁，x₂，…，x_n)，g_i(x₁，x₂，…，x_n)，(i=1，2…，m)可組成m個布爾方程，f_i(x₁，x₂，…，x_n)=g_i(x₁，x₂，…，x_n)，(i=1，2，…，m)，這m個方程所構成的方程組

稱為B上的布爾方程組。

布爾方程組的解

布爾方程組的解是布爾方程組的基本概念之一。在布爾代數B中，如果存在一個n元列a₁，a₂，…，a_n∈B滿足布爾方程組f_i(x₁，x₂，…，x_n)=g_i(x₁，x₂，…，x_n)，(i=1，2，…，m)的每個方程，則稱n元列a₁，a₂，…，a_n為布爾方程組在B中的一個特解，簡稱布爾方程組的解，而所有解的一般形式稱為通解，如布爾方程組

有通解

其中u，v，w為布爾代數中的任意元素。

相關概念

定義1 含有待定元的等式叫（相等）方程；含有待定元的不等式叫不等方程；能概括這二者的則叫廣義方程，某些（廣義）方程組成的組叫（廣義）方程組。

定義2 設是一個布爾代數，所謂上的n元布爾方程是指如下的含有n個待定元的布爾函式f(X)及g(X)所組成的等式

類似的，我們可用

及

分別定義布爾不等方程及（廣義）布爾方程組，其中“”既可以是“=”，也可以是“≤”。

布爾方程(1)的（特）解，是指滿足(1)的一個向量X∈；布爾不等方程(2)及（廣義）布爾方程組(3)的（特）解的定義類似。

定義3 若h(X)是布爾函式，k(X)=h'(X)，則

及

分別稱為（布爾）0方程與（布爾）1方程；它們又合稱為（布爾）0-1方程或0-1布爾方程。

相關定理

引理1 每一個形如(1)的布爾方程都可等價於一個0-1布爾方程。

引理2 每一個形如(2)的布爾不等方程也等價於一個0-1布爾方程。

引理3 每一個布爾0方程組

或布爾1方程組

也等價於一個0-1布爾方程。

注意，引理1，2，3都已給出了化成等價0 -1布爾方程的方法。

定理1 每一個形如(3)的廣義布爾方程（m=1的情況）或廣義布爾方程組（m>1的情況）都等價於一個0-1布爾方程。

證 (1)m=1的情況已由引理1及引理2證得；

(2)僅證m>1的情況：由於通過求補對偶變換可將0方程變成1方程，也可將1方程變成0方程，所以每一個廣義布爾方程組都可以變成0方程組或1方程組，於是再由引理53即得證。

【例1】將布爾方程組

變成與之等價的0方程。

解 (6)等價於 (xy')(ab')∪(xy')(ab')=0 ， (8)

(7)等價於 (x'y)(a’b)∪(x'y)(a'b)=0 ， (9)

(8)與(9)等價於:

[(xy')(ab')∪(xy')'(ab’)]∪[(x'y)(a'b)∪(x’y)(a'b)]=0

即

(a’b∪ab')xy∪(a'∪b)xy'∪(a∪b')x'y∪(ab'∪a'b)x'y'=0， (10)

(10)即為所求的0方程。