布爾值集全域(universe of Boolean-valuedsets)利用布爾代數對集合全域V的一種擴充。
布爾值集全域(universe of Boolean-valuedsets)利用布爾代數對集合全域V的一種擴充.在某個論域上,集合與其特徵函式具有一一對應關係,通常可把它們等同看待.如果把特徵函式的值域擴充為一個布爾代數,那么同一個集合將有多個特徵函式與其對應.利用這種方法可將集合全域V進行“擴張”.形式地講,設B為一個布爾代數,對序數a,遞歸定義vacs,為滿足下列條件的函式f的全體:
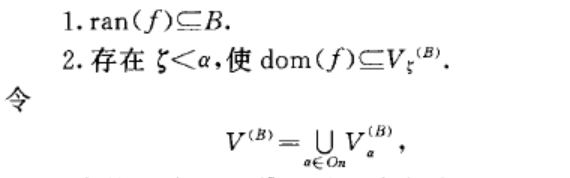
On為序數全域,稱vca>為關於布爾代數B的布爾值集全域,v<a>的元素稱為布爾值集,顯然,若布爾代數B不同,則相應的布爾值集全域v<a>也不同.若B為一個二值布爾代數2,則vcz,具有類似於V的性質.事實上,對每個二EV,定義x={(夕}1):yE對,則xE儼z}.映射x H x為V到V `z'的一一映射,且對任何公式抓xm xz , ..,二,),有抓x1 }xz, "..,,x,})成立,若且唯若v<zy} }C.i, } .xz , ... , .x‑ ).由於v<z} cv<a>,因此vca}可以被看成是對V的一種擴充,對每個xEV,稱xEV`B>為v<e>的標準元.必須指出,這裡所說的擴充只是模型論意義上的擴充,因為vca>為V的子類.
