布拉施克度量(Blaschke metric)仿射空間中超曲面上的仿射不變的黎曼度量.設M是n}-1維仿射空間中的超曲面，二是位置向量，}u' }u2, ".. }u"}}是局部坐標.
基本介紹
- 中文名：布拉施克度量
- 外文名：Blaschke metric
若
布拉施克度量
在M上定義了一個仿射不變的偽黎曼度量，稱為布拉施克度量.當M局部嚴格凸時，可選擇M的定向，使布拉施克度量正定.
布拉施克度量
相關詞條
- 布拉施克度量
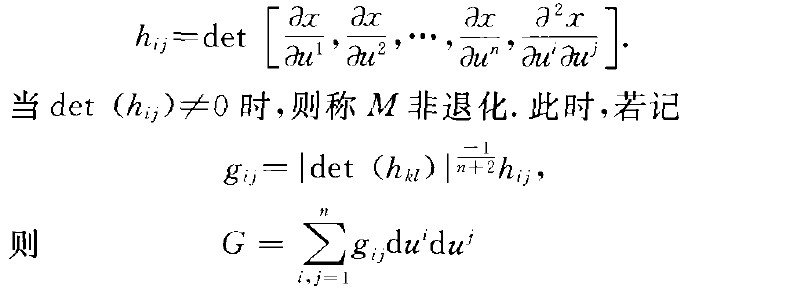
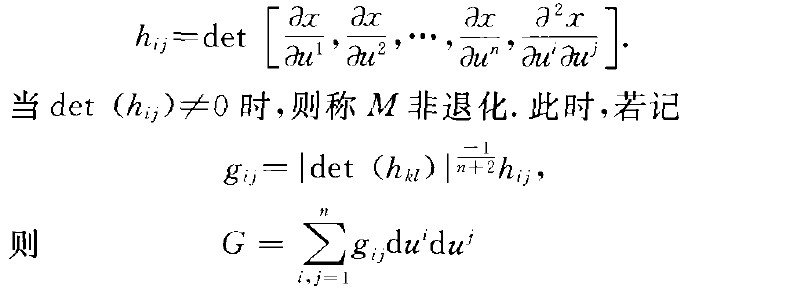
布拉施克度量(Blaschke metric)仿射空間中超曲面上的仿射不變的黎曼度量.設M是n}-1維仿射空間中的超曲面，二是位置向量，}u' }u2, ".. }u"}}是局部坐標.若在M上定義了一個仿射不變的...
- 布拉施克
它表明了任 何一個包含在一個有界集中的凸集序列必有一個子列,其關於豪斯多夫度量而言 是收斂的。這個結果一直是建立凸體所滿足的嚴格等周型不等式的有用工具。 布拉施克也闡述了所謂的布拉施克桑塔洛不等式,這是關於凸體的一個 基本的仿射幾何不等式。它與機率論和泛函分析,也與數論、偏微分方程和微分幾 ...
- 仿射球面
因此，對仿射球面的分類是基本的、重要的.關於布拉施克度量完備的局部嚴格凸仿射球面的整體分類始於布拉施克(Blaschke，W.J.E.)，他於1923年證明：一個緊緻無邊的2維球面一定是橢球面.後來，戴克(Deicke，A.)於1953年把這個結果推廣到了高維。因為完備的橢圓型仿射球面一定是緊緻無邊的，他們實際上完成了對完備...
- 仿射微分幾何基本定理
仿射微分幾何基本定理(fundamental theoremof affine differential geometry)關於仿射空間中的超曲面完全由布拉施克度量和富比尼一皮克形式確定的定理.設在一個n維單連通可微流形M上給定了黎曼度量G和一個三階對稱協變張量場A,若它們滿足一組所謂可積性條件,則存在一個從M到n+1維仿射空間A +‘的局部嚴格凸浸人二,...
- 仿射極大曲面
其中乙為布拉施克度量的拉普拉斯運算元.橢圓拋物面是仿射極大曲面的重要例子.類似於歐氏曲面論的伯恩施坦問題，陳省身於1971年提出以下猜測:定義在整個A“上的嚴格凸函式，若它的圖是仿射極大曲面，則它是二次多項式.局部的仿射曲面的例子很多，但關於布拉施克度量完備的仿射極大曲面，已知的例子只有橢圓拋物面.卡拉比(...
- 仿射法線
若M是n+1維仿射空間A中的非退化超曲面，x是位置向量，Δ是關於布拉施克度量的拉普拉斯運算元，則Y=Δx/n是M上仿射不變的橫截向量場，稱為M的仿射法向量場。過M的點x且平行於Y(x)的直線，稱為M在點x的仿射法線。當M嚴格凸時，仿射法線有下述幾何意義：用TₓM表示M在點x的切超平面，A中平行於TₓM的...
- 富比尼一皮克形式
富比尼一皮克形式(Fubini-Pick form)仿射超曲面上一個仿射不變的三次微分式.設M是、十1維仿射空間A＞ ,_‘中的非退化超曲面，Cul u2, “.. purr是局部坐標.M上可以定義兩個聯絡:一個為A..+的聯絡通過仿射法線在M上的誘導聯絡，用rkrJ表其聯絡係數;另一個是M上布拉施克度量的列維-齊維塔聯絡，用幾表其...
- 仿射微分幾何學
仿射微分幾何學(affine ldifferential geometry)是一門古典的微分幾何，屬於微分幾何學的一個分支，從屬於仿射變換群。內容包括曲線和曲面在仿射變換群下的不變數、協變圖形及其性質等，它興起於20世紀20年代初，由德國數學家布拉施克等人創建。基本內容 仿射微分幾何學是微分幾何學的一個分支，從屬於仿射變換群。內容...
- 哈代空間
這裡c為實數，B(z)為布拉施克乘積，S(z)為奇異內函式。內函式與不變子空間有密切的聯繫。令S為 的位移運算元，即S(f)=zf(z)，f∈ 。的一個子空間M稱為在S下不變，若zM⊂M。1949年，博靈(Beurling，A.)證明了下面的著名定理：H的子空間M在S下不變的充分必要條件是存在內函式G，使得：此定理在泛函...
