布勃諾夫-伽遼金法

求解齊次邊界條件彈性力學問題的一種近似方法，是俄國的И．Г．布勃諾夫於1913年首先提出，後由В．Г．伽遼金推廣套用，故得名。

基本介紹

• 中文名：布勃諾夫-伽遼金法
• 外文名：Bubnov-Galerkin me-thod
• 範圍：彈性力學
• 性質：方法

正文

此法的要點是：假定彈性體內沿x、y、z方向的位移u、v、w分別由一系列滿足彈性體的全部位移和力的邊界條件的連續函式u_i(x，y，z)、v_i(x，y，z)、w_i(x，y，z) (i=1，2，…，n)疊加而成，即

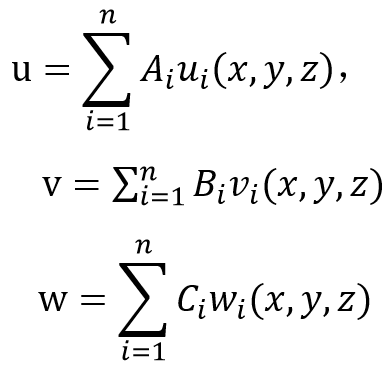
式中的A_i，B_i、C_i為待求常數，共3n個。根據虛功原理，則有：

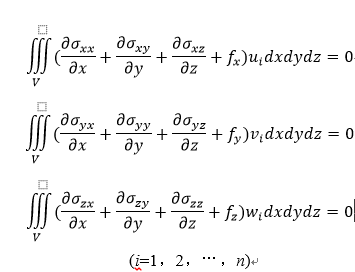
此方程紹通常稱為布勃諾夫-伽遼金方程組。式中的V為整個彈性體的體積；f_x、f_y、f_z為體積力分量；σ_xx、σ_xy、σ_yx、σ_yy、σ_xz、σ_zy、為彈性體內的應力分量；而三個括弧巾的量分別為x、y、z三個方向力的和。通過應力-應變關係和應變-位移關係可將方程組中的全部應力分量化成位移分量，而後將三個位移表達式代入積分便得到3n個關於待求係數，，（i=1，2，……，n）的代數方程，解出3n個未知係數即得到位移u、v、w。通過微分並利用應力-應變關係即可得到彈性體內的應力。這一方法已被廣泛用來解彈性力學的各種問題特別是非線性問題，其優點是只需知道物體內的平衡方程，而不必導出能量表達式。但有時難以找到既能滿足力的邊界條件又能滿足位移邊界條件的位移變化函式，因而這一方法的套用範圍受到限制。