巴特勒-福爾默方程式

巴特勒–褔爾默方程（英語：Butler–Volmer equation），也稱為埃爾第-格魯茲–福爾默方程（Erdey-Grúz–Volmer equation），是電化學領域的一個最基本的動力學關係。它描述了電極上的電流如何隨電極電勢變化，考慮到陰極方向（cathodic）和陽極方向（anodic）的反應會出現在同一個電極上。

基本介紹

• 中文名：巴特勒-福爾默方程式
• 外文名：Butler–Volmer equation
• 領域：電化學

簡介

巴特勒–褔爾默方程（英語：Butler–Volmer equation），也稱為埃爾第-格魯茲–福爾默方程（Erdey-Grúz–Volmer equation），是電化學領域的一個最基本的動力學關係。它描述了電極上的電流如何隨電極電勢變化，考慮到陰極方向（cathodic）和陽極方向（anodic）的反應會出現在同一個電極上：

或者更緊湊地寫為：

其中：：電極的電流密度，A/m（定義為i = I/A），：交換電流密度，A/m，：電極電勢，：平衡態電勢，T：熱力學溫度，z：該電極反應中涉及的電子數目，F：法拉第常數，R：氣體常數，：正極（陰極）方向電荷傳遞係數，無量綱：負極（陽極）方向電荷傳遞係數，無量綱，：活化過電位（定義為）。

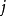
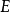
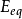
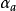
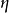
該方程的名字是為了紀念化學家約翰·阿爾弗雷德·瓦倫丁·巴特勒和馬克斯·褔爾默。

極限情況

在兩種極限情況下，巴特勒-褔爾默公式有如下形式：

低過電勢區間（即當 E≈E_eq時；此時稱為“極化電阻”），巴特勒-褔爾默公式簡化為：

高過電勢區間，此時巴特勒-褔爾默公式簡化為塔菲爾公式：

對陰極方向的反應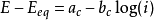，，當 E<<E_eq時

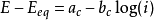
對陽極方向的反應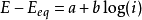，，當 E>>E_eq時

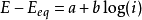
其中a和b是常量（對於某反應、在某溫度下），被稱為塔菲爾方程常數。對於陰極方向和陽極方向的反應過程，a和b的理論值是不同的。

參見

• Advanced Simulation Library軟體
  
• 能斯特方程
  
• 戈德曼方程