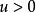尖點型突變

尖點型突變(the cusp catastrophe)是較簡單的且套用廣泛的基本突變模型，它的勢函式為V(x)=x⁴+ux²+vx，平衡曲面M的方程為4x³+2ux+v=0，分歧集為8u³+27v²=0，它由DV(x)=4x³+2ux+v=0,D²V(x)=12x²+2u=0組成的方程組消去x得到。

基本介紹

• 中文名：尖點型突變
• 外文名：the cusp catastrophe
• 所屬學科：數學（突變理論）
• 簡介：簡單的且套用廣泛的基本突變模型

基本介紹

自然界與社會現象中一般的不連續突變問題，都可歸屬於基本突變模型所刻畫，由其特定的幾何形狀表示，故探討突變問題就必須按研究基本突變模型的幾何形狀。

當具有兩個控制變數時，最簡單的突變模型為尖點型；由於其比較簡單，臨界曲面也容易構造，且幾何直觀性強，故屬套用最廣泛的突變模型。

尖點突變的幾何形狀

尖點突變，Thorn又稱為Rienan-Hugonioc點突變，其勢函式為

故相空間為狀態變數x以及u、v兩個控制變數構成的三維空間；該勢函式的臨界點為方程的解。故平衡曲面M亦由該方程給出，即

其奇點集所相應的方程為，即

將式(2)、式(3)聯立求解，消去x則可獲得分歧集方程，即判別式△

描述平衡曲面的方程式(2)是一個3次方程，該類方程或有一實根，或有3個實根，實根的數目和性質可由判別式△和u、v是否取零值而定。將平衡曲面繪出，如圖1所示。設系統的狀態是以x、u，v為坐標的三維空間中的一點所代表，則相點必定位於該曲面上，且總是位於曲面的頂葉或底葉，因為中葉是對應於不穩定平衡。

圖1

平衡超曲面M在控制平面C即u-v中的投影是一種拓撲變換或映射，可用f表示為

即

u、v的平穩變化一般都引起x的平穩變化。僅當控制點(u，v)越過分歧集時，將使x產生不連續的突變，亦即如果相點恰好在M曲面終止的邊緣上(曲面回折面形成中葉處)，則它必定跳躍到另一葉上，這引起x的突變，並產生滯後現象。尖點之中有兩個極小點，它們被一個極大點分隔，而尖點之外只有一個極小點，如圖1所示。另外，由於當時，v的變化只引起x的光滑變化，故稱為正則性態。相應地稱v為正則因子。但當u減少到負值時，即時就分裂了M，出現摺疊，x的變化不再連續，故稱u為剖分因子。