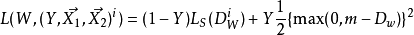對比損失

對比損失是一種降維學習方法，它可以學習一種映射關係，這種映射關係可以使得在高維空間中，相同類別但距離較遠的點，通過函式映射到低維空間後，距離變近，不同類別但距離都較近的點，通過映射後再低維空間變得更遠。這樣的結果就是，在低維空間，同一種類的點會產生聚類的效果，不同種類的mean會隔開。類似fisher降維，但fisher降維不具有out-of-sample extension的效果，不能對new sample進行作用。

基本介紹

• 中文名：對比損失
• 外文名：Contrasive Loss
• 本質：一種降維學習方法
• 作用：學習映射關係

為什麼需要對比損失函式

傳統上，維度減小包括將一組高維輸入點映射到低維manifold上，使得輸入空間中的“相似”點被映射到manifold上的附近點。經典的降維方法是主成分分析（PCA）和多維縮放（MDS）。 PCA將樣本點投影到子空間中，其中樣本點的方差最小化。 MDS將樣本投影到子空間中，該子空間最好保留輸入點之間的成對距離。另一種降維方法是ISOMAP和局部線性嵌入（LLE）。所有上述方法都預先假定輸入空間中存在有意義的度量，計算過程通常有三個步驟：1。識別每個點的鄰域列表。 2.使用該信息計算克矩陣。 3.該矩陣求解了特徵值問題。

這些方法都沒有嘗試計算可以映射新的未知數據點的函式，而無需重新計算整個嵌入，也不知道它與訓練點的關係。

優點

1. 它只需要訓練樣本之間的鄰域關係。 這些關係可能來自先前知識或手動標記，並且與任何距離度量無關。
2. 它可以學習對輸入的複雜非線性結構不變的函式，例如照明變化和幾何失真。
3. 學習的函式可用於映射在訓練期間未見的新樣本，而沒有先驗知識。
4. 由函式生成的映射在某種意義上是“平滑的”並且在輸出空間中是連貫的。

原理

讓我們考慮一對樣本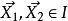 令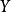 是分配給該對的二進制標籤。如果 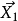和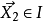 被認為是相似的，則 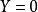，如果認為它們不相同，則 。在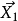 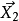， 之間定義要學習的參數化距離函式，作為 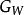輸出之間的歐氏距離。那是：

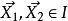
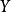
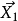
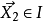
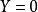
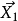
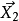
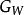
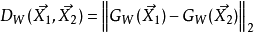
一般形式是：

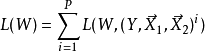
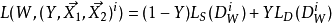
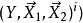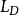其中 是標記的樣本對，是標記的樣本對，是部分失效對象的相似點，是不相似點的部分損失函式，P是訓練對的數量（可以與樣本數的平方一樣大）。

和必須設計成使得相對於WW最小化將導致類似對的值較低而不相似對的值較高。

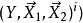
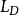
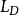
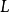
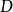
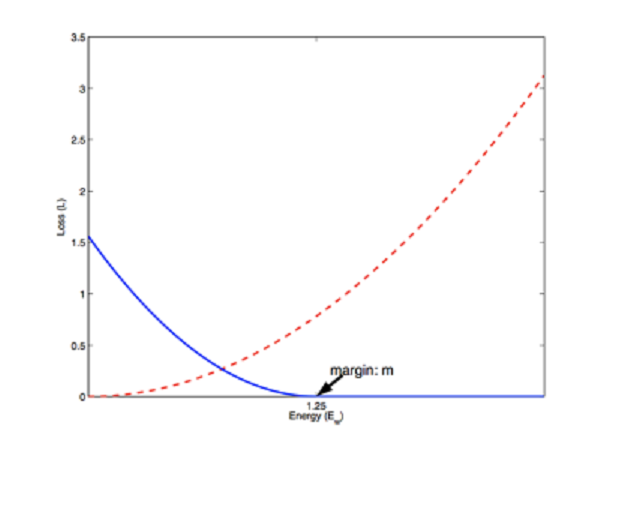
例如，最後的損失函式是：