對棱二面角

對棱二面角(opposite dihedral angle)亦稱對頂二面角，指兩個位置相關的二面角，一個二面角和反面伸展這個二面角的兩個面所成的二面角，稱為對棱二面角。

基本介紹

• 中文名：對棱二面角
• 外文名：opposite dihedral angle
• 所屬學科：數學
• 所屬問題：立體幾何（二面角）
• 別名：對頂二面角

基本介紹

當兩平面交於一直線時，構成如圖1所示的四個二面角，其中不相鄰的兩對二面角相互稱為對棱二面角。這同兩直線相交而成的四個角中的對頂角是對應的。或者說如果兩個二面角中，一個二面角的兩個面是由另一個二面角的兩個面分別延展得來的，就稱這兩個二面角為對棱二面角。

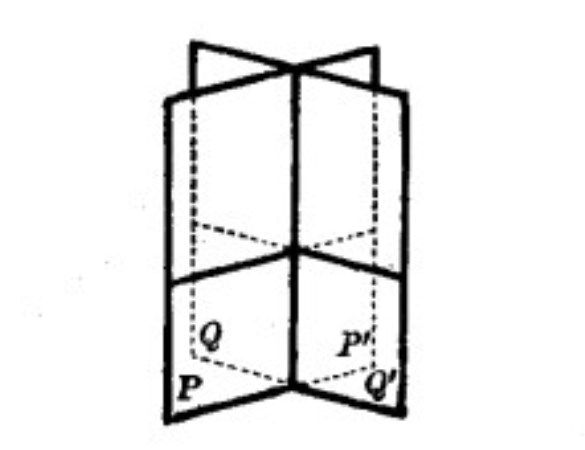
易知，對棱二面角的平面角互為對頂角，兩個對棱二面角是相等的。如圖2，設P、P'、Q、Q'為半平面。二面角“P-AB-Q”與二面角“P'-AB-Q'”就是對棱二面角。同樣，二面角“P-AB-Q'”與二面角“P'-AB-Q”也是對棱二面角。

相關性質

1.兩個對棱二面角是相等的，因為它們的平面角是對頂角。

2.兩平面相交，組成四個二面角，兩兩對棱。當其中相鄰的二面角相等(每個都是直二面角)時，兩平面稱為互(相)垂(直)。

3.兩個對棱二面角有同向，如果在公共棱上選取同一指向，並且把一個的第一面，取為另一個的第一面的延展面的話，這來源於兩個對頂角有相同的轉向。

4.通過已知平面的一條垂線的平面必垂直於已知面。

系 垂直於平面上一直線的平面，必垂直於該平面。