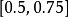對分法

對分法是用於單因素問題的一種具體優選方法。重複地在因素變化連續範圍的中點進行試驗以取得最優方案的方法。當一個實際問題依賴某一因素，而該因素的變化範圍是可確定的區間 〔a，b〕 時，就可以用對分法找到解決這個問題的最佳方案。其優點在於：在不知道該實際問題的函式關係時，只需按一定程式做最少的試驗就能成功。

基本介紹

• 中文名：對分法
• 外文名：Bisection Method
• 對分法的套用：把它分成兩部分元素個數儘量相等
• 數學家所關注：數字0.618…
• 實驗法：直到取得最理想的結果
• 別名：二分法

算法

若要求已知函式的根 (x的解)，則：

先找出一個區間，使得 與 異號。根據介值定理，這個區間內一定包含著方程式的根。

求該區間的中點，並找出 的值。

若 與 正負號相同則取 為新的區間， 否則取 .

重複第2和第3步至理想精確度為止。

例子

例: 求方程 的解, 其中 sinh 是雙曲正弦、cos 是餘弦及x以弧度量度.

定義 。因此這裡是要求f(x) = 0 的根。

畫出可大約得知其根約在 0.5 和 1 之間，故使初始區間的。

此區間之中點為 0.75。

因，其正負號不同，故令新區間為

又新區間的中點為 0.625, 而, 與f(0.5) 正負號相同，故新區間為。

不斷重複運算即得的根約為 0.7033。

偽代碼

輸入的定義輸入 a 和 b 為初始區間輸入 e 為目標誤差重複如下: 如果 則 否則 直至。

套用

題乾：一個數字介於1000000與9999999之間，要準確猜出這個數字是多少，甲提問，乙問答“是”或者“不是”，而乙知道答案，但是乙只能回答說的那個數和答案的大小關係。問甲問多少次，一定可以猜出這個數字是多少？

解答：要確定1000000與9999999之間的任何一個數，只需要問24次就行，這簡直是難以置信。然而，只要你略微懂得一點數學中對分法 的知識，就不必懷疑它的可能性了。

很明顯，問一次可以確定二元組中的一個元素。四元組問二次即可，八元組問三次，十六元組問四次，一般地說，問n次可以辨別出 2的n次方元組裡的任何一個選定的元素。

對分法優選法

數字0.618…更為數學家所關注，它的出現不僅解決了許多數學難題(如：十等分、五等分圓周；求18度、36度角的正弦、餘弦值等)，而且還使優選法成為可能。優選法是一種求最最佳化問題的方法。如在煉鋼時需要加入某種化學元素來增加鋼材的強度，假設已知在每噸鋼中需加某化學元素的量在1000—2000克之間，為了求得最恰當的加入量，需要在1000克與2000克這個區間中進行試驗。通常是取區間的中點(即1500克)作試驗。然後將試驗結果分別與1000克和2000克時的實驗結果作比較，從中選取強度較高的兩點作為新的區間，再取新區間的中點做試驗，再比較端點，依次下去，直到取得最理想的結果。這種實驗法稱為對分法。但這種方法並不是最快的實驗方法，如果將實驗點取在區間的0.618處，那么實驗的次數將大大減少。這種取區間的0.618處作為試驗點的方法就是一維的優選法，也稱0.618法。實踐證明，對於一個因素的問題，用“0.618法”做16次試驗就可以完成“對分法”做2500次試驗所達到的效果。