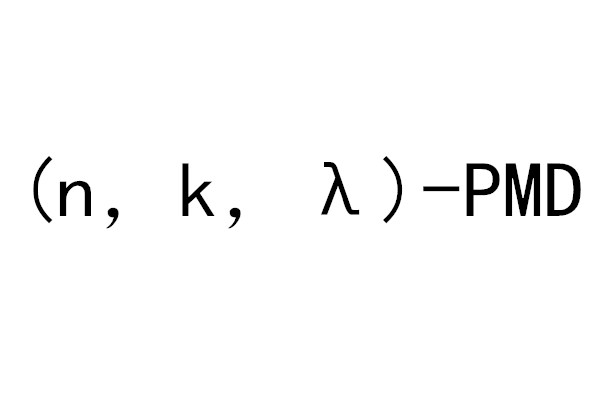完全門德爾森設計

完全門德爾森設計(perfect Mendelsohn design)是一種特殊類型的圖設計，以C'_k記k個頂點k條弧的有向圈，稱(n，k，λ)C'_k設計為門德爾森設計，簡記為(n，k，λ)-MD。若對每一個r(1≤r≤k-1)以及對任意兩個相異頂點x和y，某個(n，k，λ)-MD中恰有λ個G區組含x及y，使每一個這樣的有向圈中從x到y的有向距離為r，則稱該MD為完全門德爾森設計，記為(n，k，λ)-PMD。

基本介紹

• 中文名：完全門德爾森設計
• 外文名：perfect Mendelsohn design
• 所屬學科：數學（組合學）
• 簡介：一種特殊類型的圖設計
• 符合：(n，k，λ)-PMD

基本介紹

以記k個頂點k條弧的有向圈，稱(n，k，λ)設計為門德爾森設計，簡記為(n，k，λ)-MD。若對每一個r(1≤r≤k-1)以及對任意兩個相異頂點x和y，某個(n，k，λ)-MD中恰有λ個G區組含x及y，使每一個這樣的有向圈中從x到y的有向距離為r，則稱該MD為完全門德爾森設計，記為(n，k，λ)-PMD。

相關說明

若忽略掉G區組中頂點之間的鄰接關係而將G區組看做頂點集的一個子集，則從一個(n，k，λ)-PMD可以得到一個(n，k，λ(k-1))-BIBD。另一方面，從每一點開始按G區組的有向圈方向寫下所有k個頂點作為正交表的一行，這樣可得λn(n-1)個行，再添上λ個形如xx…x行，這裡x取遍n個頂點，於是，可得一個正交表OA(λn²，k，n，2)，特別地，當(n，k，1)-PMD存在時，也存在OA(n，k)，這等價於k-2個n階相互正交拉丁方的存在性，因此，(6，5，1)-PMD與(6，6，1)-PMD都不存在。門德爾森(N.S.Mendelsohn)證明：(n，3，λ)-PMD 存在的充分必要條件是

λn(n-1)≡0(mod 3)且(n，λ)≠(6，1).

他還首先研究了(n，4，1)-PMD，指出這樣的設計等價於滿足擬群恆等式yx·xy=x的一個n階冪等擬群。目前，當k=4，5時，(n，k，λ)-PMD的存在性已基本解決。

相關概念

G設計是平衡不完全區組設計的一種推廣，設G是有k個頂點且無孤立點的簡單無向圖，λK_n是n個頂點的λ重完全無向圖，重邊看做不同的邊，若該完全圖能分解成若干個無公共邊的子圖，每一個都與G同構，則稱這樣的分解為一個圖設計，記為(n，k，λ)G設計。當G=K_k時，一個(n，k，λ)G設計就是一個(n，k，λ)-BIBD。圖設計可以看成BIBD設計的區組中引入點之間的某種鄰接關係後的推廣，這些同構子圖稱為G區組。當G為有向圖時，將λK_n改為λ重完全有向圖λK^*_n，可類似定義(n，k，λ)G設計。當G為無向圖且(n，k，λ)G設計存在時，λn(n-1)≡0(mod 2e)且λ(n-1)≡0(mod d)，式中e是圖G的邊數而d是G的所有頂點度數的最大公因數。當G為有向圖且(n，k，λ)G設計存在時，λn(n-1)≡0(mod e)，λ(n-1)≡0(mod d⁺)且

λ(n-1)≡0(mod d^-)，

式中的e是圖G中弧的條數，而d⁺與d^-分別是所有頂點的出度數的最大公因數及入度數的最大公因數。

黑爾(P.Hell)和羅薩(A.Rosa)於1972年首先引入了圖設計這一概念，並研究了(n，k，λ)P_k設計的存在性，這裡P_k表示k個頂點k-1條邊的路，由於圖G的變化千姿百態，G設計的存在性研究面廣量大，已有結果大多是關於路和圈這些簡單而規則的圖G的，只有當k較小時才考察所有可能的圖G，而完整的結果僅限於k=3，4的情形，圖設計的直接構造方法是玻色(R.C.Bose)的對稱重差法的變形，而遞推構造方法則主要利用多部完全圖的分解，與BIBD設計的情形類似，也有可分解性問題以及平衡圖設計問題。