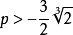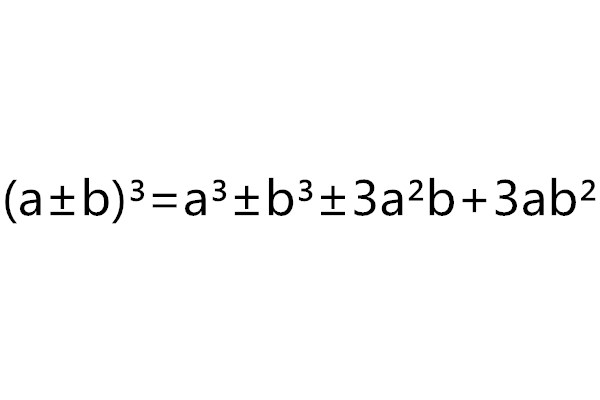完全立方式

完全立方式(perfect cube expression)是完全立方數概念的推廣，即恰好是某一代數式立方的式子，若一個代數式等於另一個代數式的立方，則這個代數式稱為另一個代數式的完全立方式，例如a±b的完全立方式是a³±b³±3a²b+3ab²。

基本介紹

• 中文名：完全立方式
• 外文名：perfect cube expression
• 所屬學科：數學
• 所屬問題：初等代數
• 重要公式：a3±b3±3a2b+3ab2=(a＋b)3

基本概念

一個數(或式子)等於某個有理數(或式子)的立方，則稱這個有理數(或式子)為完全立方數(或完全立方式)。如8=2³，8稱為完全立方數。a³﹢b³+3a²b+3ab²=(a+b)³，a³－b³－3a²b+3ab²=(a－b)³，則a³﹢b³+3a²b+3ab²和a³－b³－3a²b+3ab²為完全立方式。

完全立方式的套用舉例

化簡

【例1】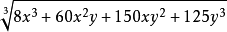

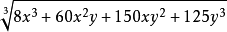
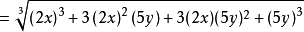
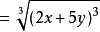
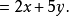
【例2】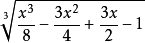

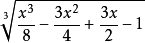
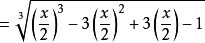
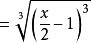
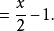
分解因式

【例3】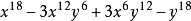

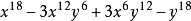
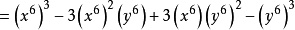
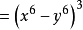
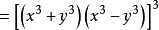
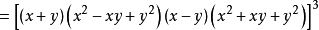
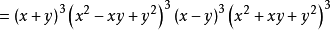
判斷根的個數

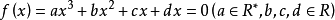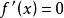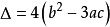定理 對於一元三次方程，設方程的判別式，則方程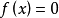的根的各種情形是：

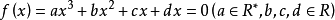
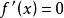
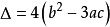
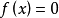
(1)方程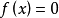有三個不同的實根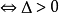且f(x)的兩個極值異號(此時，設f(x)的兩個極值點分別為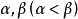，則三個根分別在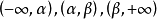內)；

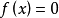
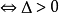
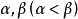
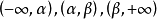
(2)方程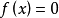有一個二重實根和一個一重實根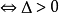且f(x)有一個極值為0(此時極值點就是二重實根)；

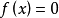
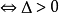
(3)方程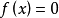有三重實根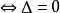(即b²=3ac)且b³=27a²d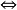f(x)是完全立方式(此時三重根為)；

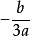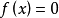
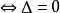
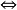
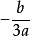
(4)方程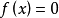有一個實根和兩個共軛虛根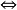除①，②，③之外的所有情形。

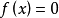
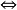
【例4】討論方程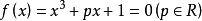的根的情況。

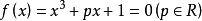
解 方程的判別式。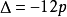

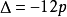
(1)當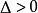且f(x)的兩個極值異號，即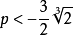時，原方程有三個相異實根；

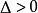
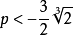
(2)當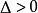且f(x)有一個極值為0，即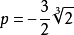時，原方程有一個二重根(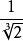)和一個一重實根()；

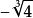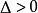
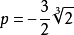
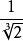
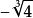
(3)f(x)不會是完全立方式，所以原方程不會有三重實根；

(4)其餘的情形，即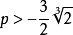時，原方程有一個實根和兩個共軛虛根。