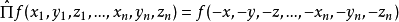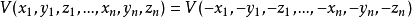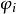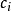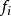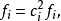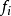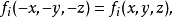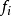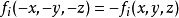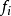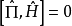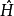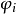宇稱算符

宇稱算符是在經典中沒有類似量的量子力學算符，宇稱是沒有經典對應的力學量。宇稱算符和哈密頓算符是可對易的。

基本介紹

• 中文名：宇稱算符
• 外文名：parity operator
• 學科：量子力學
• 特點：在經典中沒有類似量
• 性質：物理量算符
• 相關算符：哈密頓算符

概念

一些在經典中沒有類似量的量子力學算符，其中之一是宇稱算符。宇稱算符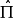 由它對任意函式f有如下的作用來定義：

宇稱算符把每個笛卡兒坐標換成其負值。例如，

如同對任何量子力學算符那樣，我們關心的是宇稱算符的本徵值和本徵函式：

問題的關鍵是計算的平方：

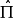
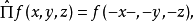
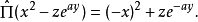
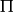
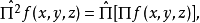
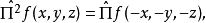
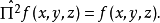
因為f是任意的。所以斷定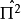是單位算符：

用作用於式，得到

因為是線性的有

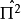
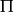
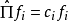
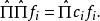
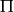
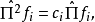
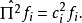
由於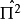是單位算符；式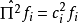為

函式不能為零(零不能作為波函式)，所以

的本徵值是+1和一1。

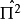
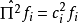
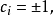
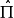
下面來考察本徵函式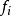。本徵方程寫為

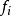
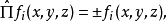
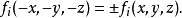
若本徵值為+1，則

是一偶函式。

若本徵值是-1，則

是一奇函式。

宇稱算符與哈密頓算符的對易關係

當宇稱算符與哈密頓算符可對易時，可選取這些算符的一個共同本徵函式集。當時，的本證函式（定態波函式）便可被選作的本證函式。

對單粒子體系，有

由於

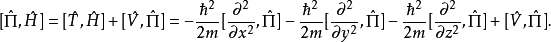
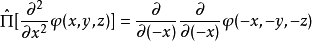
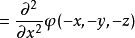
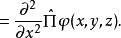
式中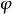是任意函式，所以

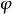
對y和z坐標的類似等式也成立，則式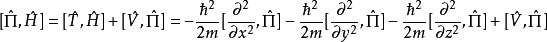變為：

有

若勢能函式是偶函式，亦即，若，則上式變為

所以。於是，當勢能函式是偶函式時，宇稱算符與哈密頓算符可對易：(V時偶函式)。

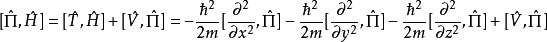
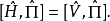
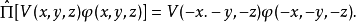
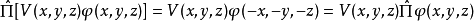
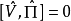
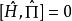
這個結果不難推廣到n粒子情況。對於一個n粒子體系，宇稱算符定義為

容易得出，當V是3n個坐標的偶函式時，即

成立時宇稱算符與哈密頓算符可對易。概括地說，當勢能V是偶函式時，宇稱算符與哈密頓算符可對易，所以可以這樣來選取波函式，使得每個不是偶函式就是奇函式。一個函式不是偶的就是奇的就說它有一定的宇稱。