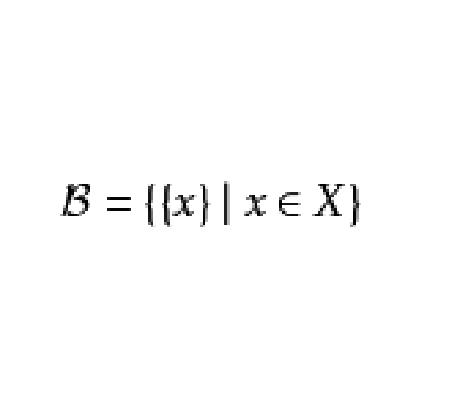子基

子基是與拓撲有關的概念。設(X,T)為拓撲空間，S⊂T，若S的元的所有有限交的族為T的基，則稱S為拓撲空間(X，T)的子基或拓撲S的子基，每一個非空集族S必是X=∪S上的某個拓撲的子基，並且該拓撲由S惟一確定，它是包含S的最小拓撲，一個拓撲可以有不同的子基，但子基確定惟一的拓撲。

基本介紹

• 中文名：子基
• 外文名：subbase
• 所屬學科：一般拓撲學
• 相關概念：拓撲、拓撲空間、基等

定義

設是拓撲空間，。若為的所有包含的拓撲的交，則稱是拓撲的子基，中的元素稱為子基開集。

等價定義為

設是拓撲空間，，若中元素的一切有限交之族是集合X上的拓撲的基，則稱是拓撲的子基，中的元素稱為子基開集。

相關概念

拓撲基

設 是拓撲空間，，若的元素都可表示為中某些元素的並，即對於，存在使得，則稱是拓撲的基或拓撲基，也稱為拓撲空間的基或拓撲基，中的元素稱為基開集。

鄰域基

設(X,τ)是拓撲空間，τ‘為X中一點x的開鄰域族。若給定包含x的任一開集U，τ‘中均存在開鄰域V⊆U，則稱τ‘為鄰域基。

例子

例1 設 是任意拓撲空間，則就是它的基。

例2 設X是非空集，記

則是集合X上的離散拓撲的基。

相關定理

定理1

設 是拓撲空間， ,則 是拓撲 的基的充分必要條件是對於任意 ，任意 ，存在 ，使得 。

證明： 必要性：對於 ，因為 是 的基，從而

其中 ，所以對於任意 ，存在 ，使得

充分性：任取 ，若 ，則取 ，從而 ，若 ，則對於任意 ，存在 使得

於是 ，記 ，因此 ，又 ，所以 是 的基。

定理2

設 是非空集X的一個子集族，則 是集合X 上的某一拓撲的基的充分必要條件是 滿足下列條件

(1) ；

(2)對於任意 是 中某些元素的並。

若 滿足上述兩個條件，則集合X上以 為基的拓撲是唯一的，此拓撲稱為以 為基生成的集合X上的拓撲。

定理3

設X為非空集， ，並且 ，則集合X上存在唯一拓撲以 為子基，這個拓撲稱為以 為子基生成的集合X上的拓撲。

證明 記

={B B是 中有限個元素的交}.

因為 ，從而 ，又對於 中任意兩個元素的交是 中元素的有限交，可見 的任意兩個元素的交屬於 ，於是這個交是 中元素的並。因此，從定理2中條件的充分性可知，集合X上有拓撲 以 為它的基，所以 是此拓撲 的子基，若 *是以 為子基的集合X上的另一拓撲，則根據子基定義， *是以為基，所以，由定理2可知 *=。

例3 設 ，則以 為子基生成的集合X上的拓撲是