基本介紹
- 中文名:子句集
- 外文名:set of clauses
- 所屬學科:數學
- 簡介:由子句構成的集合
- 相關概念:子句,文字,基子句等
定義
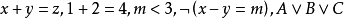

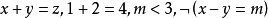
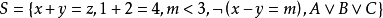
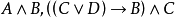
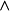

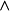
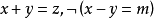
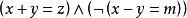
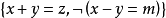
相關概念
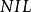
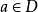
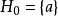
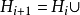
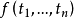
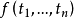
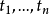
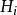
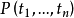
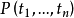
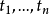
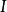
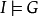
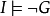
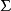
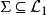
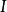
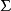
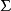
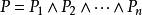
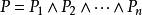

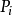


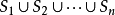
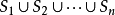

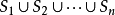

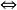
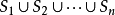
海伯倫理論
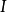


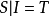

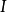
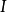

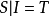


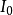
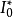

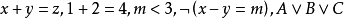

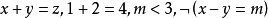
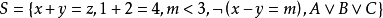
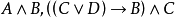
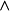

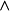
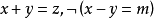
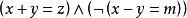
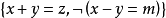
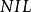
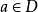
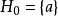
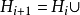
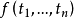
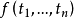
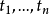
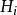
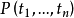
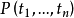
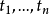
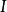
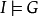
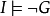
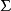
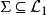
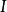
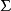
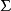
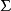
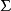
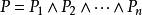
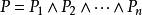

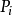


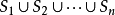
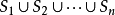

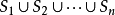

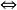
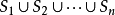
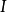


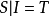

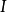
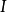

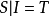


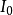
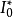
不包含變元(或變元被其定義域的元素普遍賦值後) 的文字即基礎文字(基文字)。文字以及它們的析取,都稱為子句,由子句構成的集合即子句集[1] 。...
如果一個子句中的原子公式都是基礎文字,那么它就是基礎子句(也稱基子句)。特別地,空子句是基礎子句。基礎子句的集合稱為基礎子句集(也稱基子句集)。...
設謂詞公式G的子句集為S,則按下述方法構造的個體變元域H稱為公式G或子句集S的海伯倫域(Herbrand域,簡稱H域):(1)令H0是S中所出現的常量的集合。若S中沒有...
子句S1(或文字A,或原子A)的所有變元均被H域的元素替換,這一過程稱為海伯倫化(Herbrand化,簡稱H化),H化的結果稱為一個H化基例,也稱為H化基子句S1(或H化...
如果C和D是兩個基礎子句集,並且L⊆C,M⊆D構成互補對集合,那么,基礎子句集r=r(C,D)=(C-L)∪(D-M)稱為C和D的基礎歸結原始表達式。基礎子句集S的...
,此時S也為0,即Ⅱ型的不可滿足性與子句集S的不可滿足性完全相同。如果公式G是∏∑型或∑型,此時G將有 約束的項 ,如果子句集中對於 的解釋域設定為 將與 ...
。由子句和空子句組成的集合稱為子句集。在謂詞邏輯中,任何一個謂詞公式都可以通過套用等價關係及推理規則化成相應的子句集,且子句集無量詞約束、元素只是文字的析取...
對子句集進行歸結反演時,由於事先不知道哪兩個子句可以進行歸結,更不知道通過對哪些子句對的歸結可以儘快地得到空子句,因而必須對子句集中的所有子句逐對地進行...
設C1與C2是子句集中的任意兩個子句,如果C1中的文字L1與C2中的文字L2互補,那么從C1和C2中分別消去L1和L2,並將兩個子句中餘下的部分析取,構成一個新子句C12,...
注:此定義是說,歸結的過程是在被賦值(半解釋)的子句中剔除(處於或關係中的)互補原子的過程。剔除互補原子後的子句集即基礎歸結原始表達式。...
定義7 將沒有變元出現的原子、文字、子句和子句集分別稱作基原子、基文字、基子句和基子句集。定義8 當子句集S中的某個子句C中的所有變元符號均以其H域中的...
PROLOG程式的解釋執行過程採用特定的輸入歸結,即從目標語句出發求出它和原來子句集的一個子句的歸結式(尾部和頭部匹配),新的子句再與原來子句集的一個子句求歸結...
虛子對自身的子女做出這樣的評價:「私の方から勧めたのは、星野立子一人である」(『晴子句集』序文)。對於立子評價很高。山本健吉說日常語の使用和口語性的...
1.3人類智慧型與人工智慧 4.1.1子句集的求取 7.2.2基於謂詞邏輯規劃的基本過程 1.3.1研究認知過程的任務 4.1.2消解推理規則 7.3STRIPS規劃系統 1.3.2智慧型信...
