威佐夫博弈(Wythoff's game):有兩堆各若干個物品,兩個人輪流從任一堆取至少一個或同時從兩堆中取同樣多的物品,規定每次至少取一個,多者不限,最後取光者得勝。
基本介紹
- 中文名:威佐夫博弈
- 外文名:Wythoff's game
- 領域:數學領域
- 性質:證明題
具體內容,奇異局勢的性質,證明過程,方法一,方法二,結論:,
具體內容
威佐夫博弈(Wythoff's game):有兩堆各若干個物品,兩個人輪流從某一堆取至少一個或同時從兩堆中取同樣多的物品,規定每次至少取一個,多者不限,最後取光者得勝。
這種情況下是頗為複雜的。我們用(a[k],b[k])(a[k] ≤ b[k] ,k=0,1,2,...,n)表示兩堆物品的數量並稱其為局勢,如果甲面對(0,0),那么甲已經輸了,這種局勢我們稱為奇異局勢。前幾個奇異局勢是:(0,0)、(1,2)、(3,5)、(4,7)、(6,10)、(8,13)、(9,15)、(11,18)、(12,20)。(註:k表示奇異局勢的序號, 第一個奇異局勢k=0)
可以看出,a[0]=b[0]=0,a[k]是未在前面出現過的最小自然數,而 b[k]= a[k] + k。
奇異局勢的性質
1。任何自然數都包含在一個且僅有一個奇異局勢中。
由於a[k]是未在前面出現過的最小自然數,所以有a[k] > a[k-1] ,而 b[k]= a[k] + k > a[k-1] + k > a[k-1] + k - 1 = b[k-1] > a[k-1] 。所以性質1成立。
2。任意操作都可將奇異局勢變為非奇異局勢。
事實上,若只改變奇異局勢(a[k],b[k])的某一個分量,那么另一個分量不可能在其他奇異局勢中,所以必然是非奇異局勢。如果使(a[k],b[k])的兩個分量同時減少,則由於其差不變,且不可能是其他奇異局勢的差,因此也是非奇異局勢。
3。採用適當的方法,可以將非奇異局勢變為奇異局勢。
假設面對的局勢是(a,b),若 b = a,則同時從兩堆中取走 a 個物體,就變為了奇異局勢(0,0);如果a = a[k] ,b > b[k] 那么,取走b - b[k]個物體,即變為奇異局勢;如果 a = a[k] , b < b[k] 則同時從兩堆中拿走a-a[b-a](註:這裡b-a是a的下標, 不是a*(b-a)) 個物體變為奇異局勢( a[b-a], b-a+a[b-a]);如果a > a[k] ,b= a[k] + k 則從第一堆中拿走多餘的數量a - a[k] 即可;如果a < a[k] ,b= b[k],分兩種情況,第一種,a=a[n] (n< k)從第二堆裡面拿走 b - b[n] 即可;第二種,a=b[n] (n < k)從第二堆裡面拿走 b - a[n] 即可。
證明過程
方法一
簡單分析一下,容易知道兩堆石頭地位是一樣的,我們用餘下的石子數(a,b)來表示狀態,並畫在平面直角坐標繫上。
用之前的定理:有限個結點的無迴路有向圖有唯一的核 中所述的方法尋找必敗態。先標出(0,0),然後划去所有(0,k),(k,0),(k,k)的格點;然後找y=x上方未被划去的格點,標出(1,2),然後划去(1,k),(k,2),(1+k,2+k),同時標出對稱點(2,1),划去(2,k),(1,k),(2+k,1+k);然後在未被划去的點中在y=x上方再找出(3,5)。。。按照這樣的方法做下去,如果只列出a<=b的必敗態的話,前面的一些是(0,0),(1,2),(3,5),(4,7),(6,10),…
接下來就是找規律的過程了,可能很辛苦,但是我寫得也不容易,而且我暫時沒有看到其他地方有這樣的證明過程。
忽略(0,0),記第n組必敗態為(a[n],b[n])
命題一:a[n+1]=前n組必敗態中未出現過的最小正整數
[分析]:如果a[n+1]不是未出現的數中最小的,那么可以從a[n+1]的狀態走到一個使a[n+1]更小的狀態,和我們的尋找方法矛盾。
命題二:b[n]=a[n]+n
[分析]:歸納法:若前k個必敗態分別為(a[k],a[k]+k),下證:第k+1個必敗態為(a[k+1],a[k+1]+k+1)
從該第k+1個必敗態出發,一共可能走向三類狀態,從左邊堆拿走一些,從右邊堆拿走一些,或者從兩堆中拿走一些.下面證明這三類都是勝態.
情況一:由命題一,任意一個比a[k+1]小的數都在之前的必敗態中出現過,一旦把左邊堆拿少了,我們只要再拿成那個數相應的必敗態即可。
情況二(從右邊堆拿走不太多):這使得兩堆之間的差變小了,比如拿成了(a[k+1],a[k+1]+m),則可再拿成(a[m],a[m]+m);
情況二(從右邊堆拿走很多):使得右邊一堆比左邊一堆更少,這時類似於情況一,比如拿成了(a[k+1],a[m])(其中a[m]<a[k+1]) ,則可再拿成(a[m]+m,a[m]);
情況三:比如拿成(a[m],a[m]+k+1),則可再拿成(a[m],a[m]+m).
綜上所述,任何從(a[k+1],a[k+1]+k+1)出發走向的狀態都可以走回核中.故原命題成立.
以上兩個命題對於確定(a[n],b[n])是完備的了,給定(0,0)然後按照這兩個命題,就可以寫出(1,2),(3,5),(4,7),…
這樣我們得到了這個數列的遞推式,以下我們把這兩個命題當成是(a[n],b[n])的定義。
先證明兩個性質:
性質一:核中的a[n],b[n]遍歷所有正整數。
[分析]:由命題一,二可得a[n],b[n]是遞增的,且由a[n]的定義顯然。
性質二:A={a[n]:n=1,2,3,…},B={b[n]:n=1,2,3,…},則集合A,B不交。
[分析]:由核是內固集,顯然。
看到這裡大家有沒有想到Beatty序列呢,實際上a[n]和b[n]就是一個Beatty序列。
an=[αn],bn=[βn],有 an+n=[(α+1)n]=[βn],解方程 1/(α+1)+1/α=1
得 α=(sqrt5+1)/2,到此,我們找到了該必敗態的通項公式。
實際上這組Beatty序列還有一些別的性質,比如當一個數是Fibonacci數的時候,另一個數也是Fibonacci數;而且兩者的比值也越來越接近黃金比,這些性質在得到通項公式之後不難證明。
總的來說,這個問題給我們了哪些啟示呢?首先用定理所說的方法找核,然後給出核的規律(遞推,或是通項)並且證明。
方法二
定理 0:一個狀態是必敗態,若且唯若它的所有後繼狀態都是必勝態;而一個狀態是必勝態,只要它的後繼狀態有一個以上的必敗態即可。
證明略去。
容易發現下面的定理:
定理 1:(a,b) 和 (b, a) 的勝負性是相同的(a <> b)。
證明:如果 (a, b) 是必勝態,那么將必勝策略中所有的操作,對第一堆的變為第二堆,對第二堆的變為第一堆,就構成 (b, a) 的必勝策略
定理 2:若 (a, b) 是必敗態,則對於所有的 x <> a 和 y <> b,(x, b) 和 (a, y) 是必勝態。
證明:
對於 x > a 和 y > b,不管是哪一種情況,總可以從 x 堆或 y 堆中取出一定量的石子使當前狀態變為必敗態 (a, b),由定理 1,(x, b) 和 (a, y) 為必勝態。
對於 x < a 和 y < b,不管是哪一種情況,如果 (x, b) 或 (a, y) 是必敗態的話,由上述可得 (a, b) 是必勝態,矛盾。故 (x, b) 和 (a, y) 均為為必勝態。
定理 3: 若 (a, b) 是必敗態,則對於所有的 d > 0,(a + d, b + d) 是必勝態。
證明:
與定理 2 類似。
定理 4:在所有的必敗態中,每個數字恰巧出現一次。
證明:
有了定理 1,對於對稱的狀態我們只需要處理其中一個,而兩個數不會相同(相同的狀態必然是必勝態),於是我們把每個狀態中較小的數字放在前面,每行寫一個狀態,去掉括弧並按照升序排列每行的第一個數,就構成了如下的矩陣:
1 2
3 5
4 7
6 10
……
假設數字k在矩陣中出現兩次或兩次以上,則有(k,a),(k,b)都為必敗態,與定理2矛盾。
假設數字k為序列中沒有出現且值最小的數字,則有 (k,k+i)為必勝態(i>0),則對任意i,必然存在j(0<j<k)使得(k-j,k+i-j)或(k,k+i-j)或(k-j,k+i)為必敗態 (若不如此,則無論如何取石子,對方必勝),根據假設,顯然(k,k+i-j)必勝,因此,對任意i,必有(k-j,k+i-j)或(k-j,k+i)=0, (0<j<k) 必敗
根據鴿巢原理,必然存在3個i的取值(其實是無窮多個,j只有k-1種取值,而i有無數種)記為i1, i2, i3使得j1=j2=j3=m。對這3個i,同樣必然存在一對i,不妨為(i1,i2),使(k-m,k+i1-m)且(k-m,k+i2-m)必敗或f(k-m,k+i1)且f(k-m,k+i2)必敗。顯然與定理2矛盾,因此不存在這樣的數k。
觀察這個矩陣,我們又可以得到新的定理:
定理 5:矩陣中每行第一個數恰巧是前面每一行中沒有出現過的最小正整數。
證明:
由定理 4,矩陣中每個數字恰巧出現一次,而按照這個矩陣的定義,第二列的數總比同行第一列大,第一列又按照升序排列,所以每一行的第一個數正好為前面每一行中沒有出現過的最小正整數。
定理 6:矩陣第 i 行的第二個數正好為第一個數加上 i
證明:
用數學歸納法。
1) 對於第一行顯然成立
2) 若對於前 i - 1 行均成立,則所有的 (a[p], a[p] + p) (a[p] 為第 p 行第一個數,p < i) 均為必敗態,那么考察第 i 行的狀態 (a[i], a[i] + delta)。容易看出 delta >= i,因為如果 delta < i,一定可以通過一次操作變為前面出現過的必敗態,那么這個狀態就是必勝態。下面由 delta >= i,我們來說明 delta = i。
首先,我們考慮從第一堆中取出 p 個石子,得到狀態 (a[i] - p, a[i] - p + delta),由定理 5,比 a[i] 小的數都在之前出現過,若 a[i] - p 出現在某一行的第一列,由於存在必敗態 (a[i] - p, a[i] - p + d) (d < delta),故 (a[i] - p, a[i] - p + delta) 一定為必勝態(定理 2);若 a[i] - p 出現 在某一行的第二列,由於第一列是單增的,因而其對應的第一列數必小於 a[i] + delta,故而也可推出其狀態為必勝態。
在某一行的第二列,由於第一列是單增的,因而其對應的第一列數必小於 a[i] + delta,故而也可推出其狀態為必勝態。

對於從兩堆石子中取出相同數目的情況與之類似,容易看出一定為必勝態。
於是,(a[i], a[i] + delta) 狀態的勝負性只與狀態 (a[i], a[i] + d) (d < delta) 有關。不難看出,delta = i 時恰為必敗態,因為不論從第二堆中取出多少個石子,作為另一堆的第一堆石子並沒有在之前出現過,所以得到的一定是一個必勝態,因而 (a[i], a[i] + delta) 為必敗態,由定理 2 及定理 4 可得,原命題成立。即矩陣中第 i 行第二列的數等於同行第一列的數加上 i。
這時,我們所有的問題都轉化到了矩陣上,只要能通過合適的方法表示出這個矩陣,我們就可以很好地解決原問題。
下面的過程可能需要比較高的數學技巧,首先給出我們需要的一個重要定理([x] 表示 x 的整數部分,{x} 表示 x 的小數部分,即 {x} = x - [x]):
定理 7(Betty 定理):如果存在正無理數 A, B 滿足 1/A + 1/B = 1,那么集合 P = { [At], t
證明:詳見Betty定理。
考慮到 Betty 定理中“恰為 Z
於是我們得到每一行第二列的數為 [
我們的目的是要讓 Z
於是套用 Betty 定理,我們得到最終我們需要的定理:
定理 8:上述矩陣中每一行第一列的數為 [
證明:由 Betty 定理顯然得證。
設a、b是正無理數且 1/a +1/b =1。記P={ 【na】 | n為任意的正整數},Q={ 【nb】 | n 為任意的正整數},則P與Q是Z+的一個劃分,即P∩Q為空集且P∪Q為正整數集合Z+。
證明:因為a、b為正且1/a +1/b=1,則a、b>1,所以對於不同的整數n,【na】各不相同,類似對b有相同的結果。因此任一個整數至多在集合P或Q中出現一次。
* 現證明P∩Q為空集;(反證法)假設k為P∩Q的一個整數,則存在正整數m、n使得【ma】=【nb】=k。即k < ma、nb<k+1,等價地改寫不等式為
* m/(k+1)< 1/a < m/k及n/(k+1)< 1/b < n/k。相加起來得 (m+n)/(k+1) < 1 < (m+n)/k,即 k < m+n < k+1。這與m、n為整數有矛盾,所以P∩Q為空集。現證明Z+=P∪Q;已知P∪Q是Z+的子集,剩下來只要證明Z+是P∪Q的子集。(反證法)假設Z+\(P∪Q)有一個元素k,則存在正整數m、n使得【ma】< k <【(m+1)a】、【nb】< k <【(n+1)b】。 由此得ma < k ≦【 (m+1)a】-1<(m+1)a -1,類似地有nb < k ≦【 (n+1)b】-1<(n+1)b -1。等價地改寫為 m/k < 1/a < (m+1)/(k+1)及n/k < 1/b < (n+1)/(k+1)。兩式加起來,得
(m+n)/k < 1 < (m+n+2)/(k+1),即m+n < k < k+1 < m+n+2。這與m, n, k皆為正整數矛盾。所以Z+=P∪Q。
補充一圖: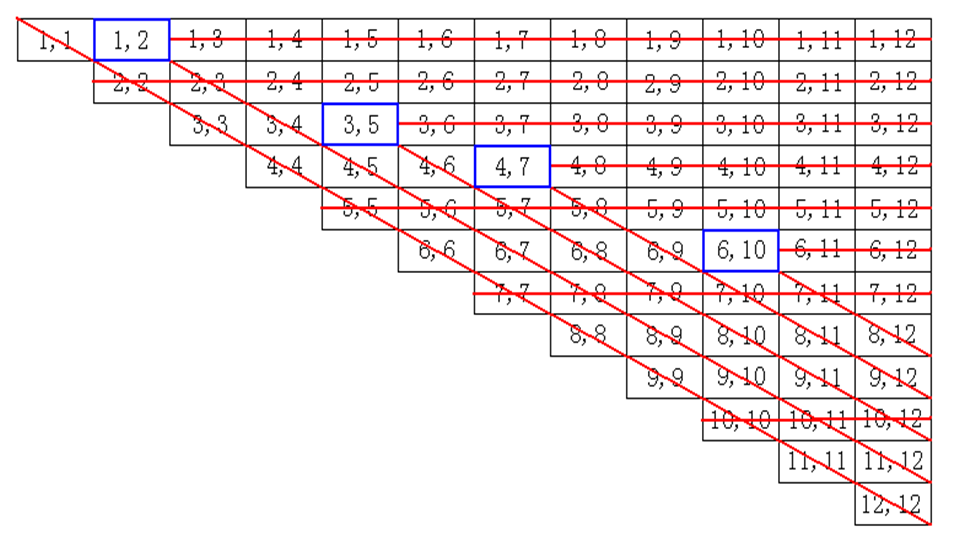

結論:
兩個人如果都採用正確操作,那么面對非奇異局勢,先拿者必勝;反之,則後拿者取勝。
那么任給一個局勢(a,b),怎樣判斷它是不是奇異局勢呢?我們有如下公式:
ak =[k(1+√5)/2],bk= ak + k (k=0,1,2,...n 方括弧表示取整函式)
奇妙的是其中出現了黃金分割數(1+√5)/2 = 1.618...因此,由ak,bk組成的矩形近似為黃金矩形,由於2/(1+√5)=(√5-1)/2,可以先求出j=[a(√5-1)/2],若a=[j(1+√5)/2],那么a = aj,bj = aj + j,若不等於,那么a = aj+1,b = aj + j + 1,若都不是,那么就不是奇異局勢。然後再按照上述法則進行,一定會遇到奇異局勢。
