奇異攝動理論自誕生以來在數學領域和控制領域中均取得了突破性進展,並隨著控制理論的發展而不斷完善。若攝動問題的解Ur(x),當r趨向於0時,不存在關於變數x一致收斂的極限,則稱為奇異攝動問題。
奇異攝動問題的類型很多,故有許多種解決各類問題的方法。奇異攝動問題作為套用數學領域的一個活躍分支,其最早的數值方法是差分方法和有限元法。然而,研究發現,在參數非常小的情況下,網路步長越小所獲解的精度越高,但網路步長太小也易引起數值不穩定現象。另外,奇異攝動問題中出現的方程往往是非對稱的,如果用通常的有限元方法求解,則不能得到正確結果。也就是說,以上常用的兩種數值計算方法解決奇異攝動問題是不適用的。因此,研究人員近30年主要專注於研究適用處理奇異攝動問題的差分方法(如擬合差分法、加權差分法和非均勻網路差分法)和廣義Galerkin方法(如迎風有限元法和指數型擬合有限元法),其中,涉及到常微分方程的初值問題和邊值問題以及偏微分方程的奇異攝動問題。
在控制領域,處理奇異攝動問題主要採用邊界層校正法,多年來,奇異攝動理論與方法以其特殊的優點,得到了國內外學者的廣泛關注,麻省理工學院、加州大學洛杉磯分校等許多國外研究機構針對機器人、過程控制系統等進行奇異攝動建模與控制研究。
基本介紹
- 中文名:奇異攝動控制
- 外文名:Singularly Perturbed Control
線性奇異攝動系統
連續時間線性奇異攝動系統

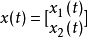








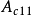

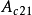
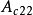


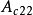
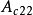
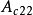
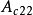
近年來,連續線性奇異攝動系統得到了充分的研究,其穩定性分析與控制研究可歸納為三種,即慢、快子系統分解方法,廣義分解法以及整體建模與設計法。
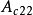
(2)廣義分解法。“廣義分解法”從廣義系統角度出發,將慢子系統描述為廣義系統,從而克服“慢、快分解法”不能處理非標準連續線性奇異攝動系統的問題。對於充分小攝動參數,廣義系統最優控制器的最優指標約等於奇異攝動系統的次優控制器的性能指標。基於Recursive方法可設汁高精度控制器¨列方法,分解Riccati方程法也可獲得攝動參數無關的

(3)整體建模與設計法。經典的慢、快子系統分解法無法處理非標準線性奇異攝動系統。而廣義系統方法的推導過程複雜,難以用線性矩陣不等式方法求解,學者們轉而研究無需分解慢、快子系統的整體建模與設計法,基於極點配置的不確定性連續奇異攝動的動態輸出反饋


具有常時延的連續時問線性奇異攝動控制系統模型為


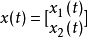







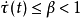





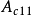

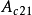
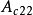


上式的慢、快變分解方法成立的前提是
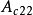
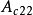
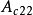
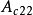
離散時問線性奇異攝動系統


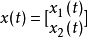




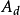


非標準離散線性奇異攝動系統模型一為



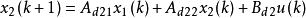

②控制器設計
相對連續奇異攝動系統控制研究而言,離散奇異攝動系統控制問題的研究較少,基於Lyapunov函式的控制方法主要有:標準線性離散奇異攝動系統的調節器問題、基於LMI方法的魯棒

經典非線性奇異攝動系統


模糊奇異攝動系統
模糊奇異攝動建模與控制法是融合模糊邏輯理論與奇異攝動技術,研究非線性奇異攝動系統的分析與控制的方法,其核心思想是針對被控對象非線性奇異攝動系統,建立含有慢、快變數的模糊奇異攝動模型,從而設計攝動參數無關或有關的控制器。採用此類方法研究的非線性奇異攝動系統,統稱為模糊奇異攝動系統。由於攝動參數的存在,模糊奇異攝動系統的分析與控制無法直接套用常規模糊系統理論與方法,否則將遇到攝動參數引起的數值求解中的病態問題。因此,模糊奇異攝動系統分析與控制方法成為研究熱點。