奇異吸子

奇異吸子（Strange attractor），也稱奇異吸引子，是具有分形結構的吸子。當動態系統發生混沌現象時，相空間分析常出現奇異吸子；然而奇異吸子也在非混沌的情形出現。若一奇異吸子是混沌的，則其對初始條件敏感。也就是任意兩個極為接近的初始點，在一定數量的疊代運算後，兩者可以相距甚遠；也可以再經過一定數量的疊代運算後又變得極為靠近。也因此，一個具有混沌吸子的動力系統在局域是不穩定，然而廣域來看卻可以是穩定的，因為這些動態點再怎么彼此分離，也都不會離開吸子。

基本介紹

• 中文名：奇異吸子
• 外文名：Strange attractor
• 領域：混沌理論
• 定義：具有分形結構的吸子
• 命名：David Ruelle與Floris Takens
• 有關術語：吸引子

簡介

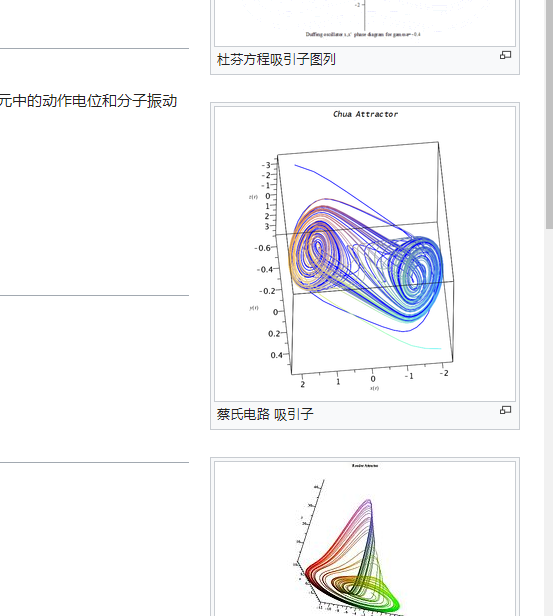
奇異吸子是反映混沌系統運動特徵的產物，也是一種混沌系統中無序穩態的運動形態。奇異吸子這個詞最早是由David Ruelle與Floris Takens所命名，用以描述流體系統經一連串分岔所產生的吸子結果。奇異吸子在一些方向上常是可微的，但一些例子則如同康托塵而不可微。奇異吸子亦可在有噪聲的場合出現。奇異吸子的例子包括多卷波混沌吸引子、艾儂吸子、熱斯勒吸子，以及洛倫茨吸子。

特點

奇異吸引子是混沌運動的主要特徵之一。奇異吸引子的出現與系統中包含某種不穩定性（不同於軌道不穩定性和李雅普諾夫不穩定性）有著密切關係，它具有不同屬性的內外兩種方向：在奇異吸引子外的一切運動都趨向（吸引）到吸引子，屬於"穩定"的方向；一切到達奇異吸引子內的運動都互相排斥，對應於"不穩定"方向。奇異吸引子的一個著名例子是洛倫茨吸引子，它是在研究天氣預報中大氣對流問題的洛倫茨模型中得到的。洛倫茨吸引子由"渾然一體"的左右兩簇構成，各自圍繞一個不動點。當運動軌道在一個簇中由外向內繞到中心附近後，就隨機地跳到另一個簇的外緣繼續向內繞，然後在達到中心附近後再突然跳回到原來的那一個簇的外緣，如此構成隨機性的來回盤旋。奇異吸引子具有兩個主要的特點：①奇異吸引子上的運動對初始值表現出較強的敏感依賴性，在初始值上的微不足道的差異，就會導致運動軌道的截然不同。②奇異吸引子往往具有非整數維（也稱分維），如2.06維、1.2365維等，常需要通過計算才能加以確定。1976年，美國物理學家M.J.費根鮑姆發現，奇異吸引子具有標度無關性。當把標尺作適當的放大後，吸引子的細節部分具有與整體相同的結構，同一種形態在越來越小的尺度上重複，其典型例子是埃農吸引子。

吸引子

吸引子是微積分和系統科學論中的一個概念。一個系統有朝某個穩態發展的趨勢，這個穩態就叫做吸引子。吸引子分為平庸吸引子和奇異吸引子。例如一個鐘擺系統，它有一個平庸吸引子，這個吸引子使鐘擺系統向停止晃動的穩態發展。平庸吸引子有不動點（平衡）、極限環（周期運動）和整數維環面（概周期運動）三種模式。而不屬於平庸的吸引子的都稱為奇異吸引子，它表現了混沌系統中非周期性，無序的系統狀態，例如天氣系統。例如，氣候就是天氣系統的奇異吸引子，由於大氣過程的複雜性和不斷地受太陽熱量等外力的驅使，導致氣候不可能被吸引到一個固定點或者一個周期性的模式中。科學家在研究混沌時常常通過編製程序和在計算機上解出基本方程而由機器把奇異吸引子畫出來，並且將其物化為顏色多樣和形狀奇異的模式。科學家們通過對奇異吸引子的探索想搞清楚，在一個混沌系統中，什麼樣的狀態可以存在，什麼樣的狀態不能存在。對於吸引子，學術上並沒有完善的定義，僅處於概念階段。吸引子中的奇異吸引子對於混沌系統的研究意義重大。

洛倫茨吸引子

洛倫茨吸引子及其導出的方程組是由愛德華·諾頓·洛倫茨於1963年發表，最初是發表在《大氣科學雜誌》（Journal of the Atmospheric Sciences）雜誌的論文《Deterministic Nonperiodic Flow》中提出的，是由大氣方程中出現的對流卷方程簡化得到的。

這一洛倫茨模型不只對非線性數學有重要性，對於氣候和天氣預報來說也有著重要的含義。行星和恆星大氣可能會表現出多種不同的準周期狀態，這些準周期狀態雖然是完全確定的，但卻容易發生突變，看起來似乎是隨機變化的，而模型對此現象有明確的表述。

從技術角度看來，洛倫茨振子具有非線性、三維性和確定性。2001年，沃里克·塔克爾（Warwick Tucker）證明出在一組確定的參數下，系統會表現出混沌行為，顯示出人們所知的奇異吸引子。這樣的奇異吸引子是豪斯多夫維數在2與3之間的分形。彼得·格拉斯伯格（Peter Grassberger）已於1983年估算出豪斯多夫維數為2.06 ± 0.01，而關聯維數為2.05 ± 0.01。

此系統也會在單模雷射和發電機的簡化模型中出現。除此之外，閉環對流、水輪轉動等物理模型也有此系統的套用。

混沌理論

混沌理論（Chaos theory）是關於非線性系統在一定參數條件下展現分岔（bifurcation）、周期運動與非周期運動相互糾纏，以至於通向某種非周期有序運動的理論。在耗散系統和保守系統中，混沌運動有不同表現，前者有吸引子，後者無（也稱含混吸引子）。

從20世紀80年代中期到20世紀末，混沌理論迅速吸引了數學、物理、工程、生態學、經濟學、氣象學、情報學等諸多領域學者有關注，引發了全球混沌熱。混沌，也寫作渾沌（比如《莊子》）。自然科學中講的混沌運動指確定性系統中展示的一種類似隨機的行為或性態。確定性（deterministic）是指方程不含隨機項的系統，也稱動力系統（dynamical system）。典型的模型有單峰映象（logistic map）疊代系統，洛倫茲微分方程系統，若斯叻吸引子，杜芬方程，蔡氏電路，陳氏吸引子等。為渾沌理論做出重要貢獻的學者有龐加萊、洛倫茲、上田睆亮（Y. Ueda）、費根堡姆、約克、李天岩、斯美爾、芒德勃羅和郝柏林等。混沌理論向前可追溯到19世紀龐加萊等人對天體力學的研究，他提出了同宿軌道、異宿軌道的概念，他也被稱為渾沌學之父。

混沌行為可以在許多自然系統中被觀測到，例如天氣和氣候。對於這個行為的研究，可以通過分析混沌數學模型，或者通過諸如遞歸圖和龐加萊映射等分析技術。