對於地球上的某個地點,太陽高度角是指太陽光的入射方向和地平面之間的夾角,專業上講太陽高度角是指某地太陽光線與通過該地與地心相連的地表切面的夾角。太陽高度角簡稱高度角。當太陽高度角為90°時,此時太陽輻射強度最大;當太陽斜射地面時,太陽輻射強度就小。
基本介紹
- 中文名:太陽高度角
- 外文名:solar elevation angle
- 性質:度角
- 正午時:太陽高度角最大(90°)
- 日出日落時:角度都為0
定義
一般時間
正午時間
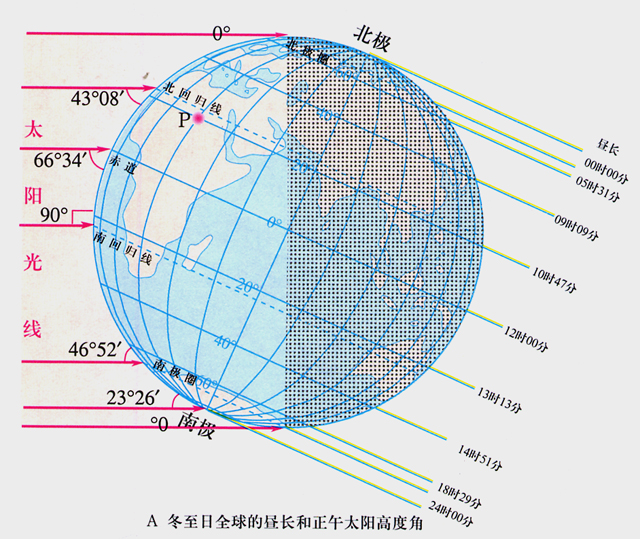 正午太陽高度角
正午太陽高度角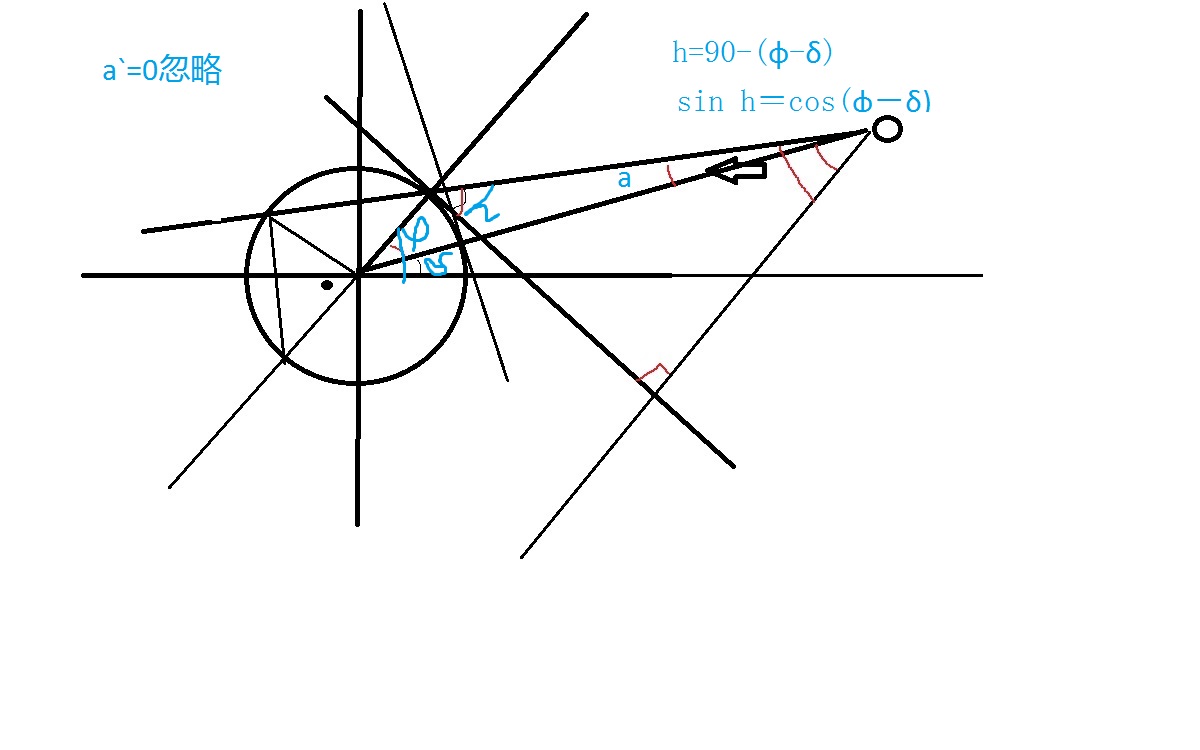 太陽高度角計算
太陽高度角計算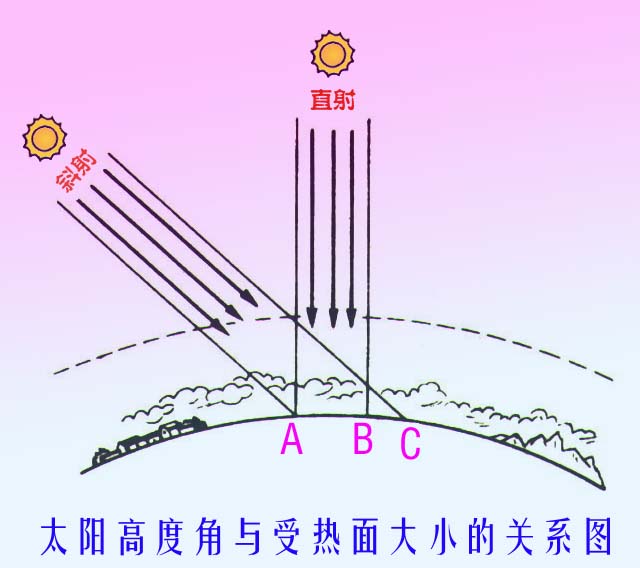

對於地球上的某個地點,太陽高度角是指太陽光的入射方向和地平面之間的夾角,專業上講太陽高度角是指某地太陽光線與通過該地與地心相連的地表切面的夾角。太陽高度角簡稱高度角。當太陽高度角為90°時,此時太陽輻射強度最大;當太陽斜射地面時,太陽輻射強度就小。
 正午太陽高度角
正午太陽高度角 太陽高度角計算
太陽高度角計算
對於地球上的某個地點,太陽高度角是指太陽光的入射方向和地平面之間的夾角,專業上講太陽高度角是指某地太陽光線與通過該地與地心相連的地表切面的夾角。太陽高度角...
高度角,即從一點至觀測目標的方向線與水平面間的夾角。是三角高程測量中計算兩點間高差的主要觀測量。太陽高度角指從太陽中心直射到當地的光線與當地水平面的夾角...
以北半球北回歸線穿過的地區為例:一年中當太陽光直射北回歸線時,正值我國北方的夏至節氣,正午太陽在頭頂正上方,即太陽高度角為90°,為一年中的最大值;當太陽...
太陽直射點是地球表面太陽光射入角度(即太陽高度角 )為90度的地點,它是地心與日心連線和地球球面的交點。 太陽直射點所在的經線的地方時為正午12時。...
太陽方位角是太陽在方位上的角度,它通常被定義為從北方延著地平線順時針量度的角。...... 太陽高度,或高度角,也就是太陽高度角是從觀測者所在地和太陽中心的聯...
太陽入射角是太陽直射光線與壁面法線之間的夾角。太陽入射角隨太陽高度角、方位、壁面方位、壁面傾斜度的不同而改變。...
太陽輻射強度是表示太陽輻射強弱的物理量,稱為太陽輻射強度。單位是W/m2,即點輻射源在給定方向上發射的在單位立體角內的輻射通量。...
太陽位置圖是太陽在天空視表面上運行軌跡的平面投影圖。太陽位置圖用平面圖形表示一年中太陽高度角、方位角與地理緯度、赤緯、時角之間的相互關係,是確定太陽空間位置...
太陽直接輻射的強弱和太陽高度角、大氣透明度、雲況、海拔高度等因素有關,其中前兩者是主要因素。(1)太陽高度角的大小不同,地表面單位面積上所獲得的太陽輻射量也...
太陽高度角大,則太陽輻射強。2.天氣狀況 晴朗的天氣,由於雲層少且薄,大氣對太陽輻射的削弱作用弱,到達地面的太陽輻射就強;陰雨的天氣,由於雲層厚且多,大氣對太陽...
即使在晝半年正午太陽高度角亦甚小,是天文輻射最小、年變化最大的地區。 [1] 太陽氣候評價 編輯 上述由天文輻射所決定的氣候稱為天文氣候,它雖反映了世界氣候...
(1)太陽高度角:太陽總輻射與太陽高度角呈正相關;(2)大氣透明度:大氣透明度差,到達地面的太陽直接輻射減少,從而減少太陽總輻射;(3)大氣質量:大氣質量越大,到達...
任一瞬間,地球各地所處的晝夜狀態可以用太陽高度來表達。太陽高度是太陽高度角的簡稱,表示太陽光線對當地地平面的傾角。在晝半球上的各地,太陽高度總是大於0度,即...
天空擴散光沒有方向性,不形成陰影,在地面上形成的照度受太陽高度角的影響較小,而受天空中的雲量、雲狀和大氣中雜質含量的影響較大。夏季晴天中午,天空擴散光照度...
式中:h—太陽高度角;H—前幢房屋女兒牆頂面至地面高度;H1—後幢房屋窗台至地面高度。(根據現行設計規範,一般H1取值為0.9m,H1>0.9m時仍按照0.9m取值)實際套用...
中國處於地球北半球、歐亞大陸東部,大部分陸地位於北歸線(北緯)以北,太陽多從東偏南升起,從西邊落下。冬季,太陽高度角較小,住宅的門、窗朝南,可使更多斜射的太...
來源數量 3個 相關概念 太陽高度角 其單位為:瓦特/平方米(W/㎡)。大氣輻照度的輻射能量有三個來源:1、太陽輻射穿過大氣圈時的散射作用;2、大氣圈本身的熱輻...
在赤道和低緯度地區,太陽高度角大,日照時間長,太陽輻射強度強,地面和大氣接受的熱量多、溫度較高;在高緯度地區太陽高度角小,日照時間短,地面和大氣接受的熱量小,...
會導致在整個地球表面所得光熱不均勻,赤道地區太陽高度角大,太陽輻射強烈,所得光熱多,而越往南北兩極地區,太陽高度角越來越小,所得光熱也很少,就導致到了高...
光合有效輻射占太陽直接輻射的比例隨太陽高度角增加而增加,最高可達45%。而在散射輻射中,光合有效輻射的比例可達60~70%之多,所以多雲天反而提高了PAR的比例。光合...
