基本介紹
- 中文名:天球坐標系統
- 外文名:celestial coordinate syatem
- 分類:地平、時角、赤道、黃道坐標系
- 要素:基本圈、次圈、極點、原點
定義
分類
地平坐標系
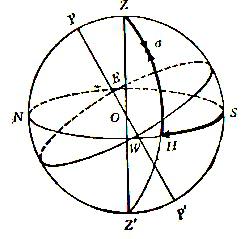 地平坐標系
地平坐標系時角坐標系
 時角坐標系
時角坐標系赤道坐標系
 赤道坐標系
赤道坐標系黃道坐標系
 黃道坐標系
黃道坐標系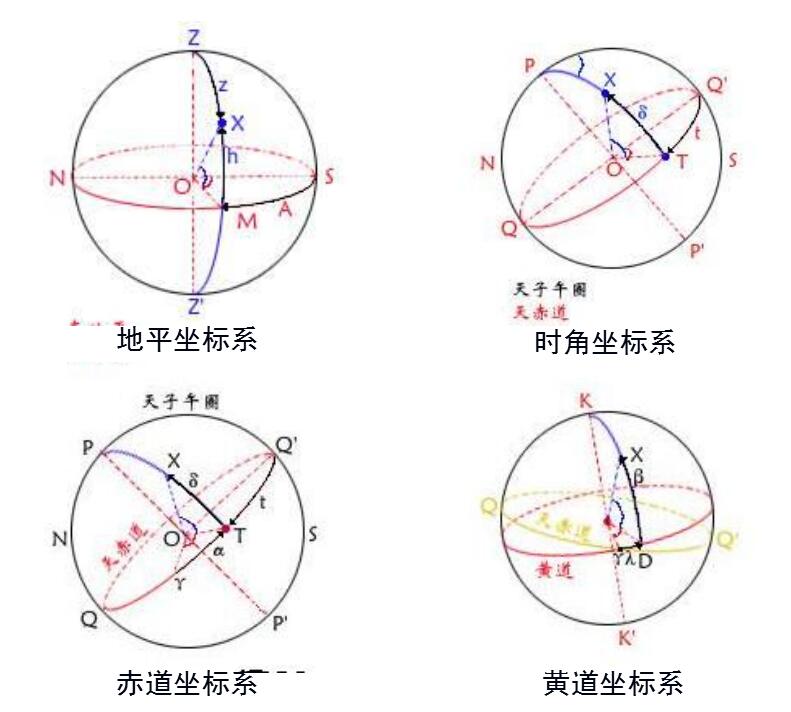
 地平坐標系
地平坐標系 時角坐標系
時角坐標系 赤道坐標系
赤道坐標系 黃道坐標系
黃道坐標系天文學當中,天球坐標系統是以球面坐標為依據,確定天體在天球上的位置而規定的坐標。球面坐標系統包括基本圈、次圈、極點和原點。常用的天球坐標系有地平坐標系、...
天球坐標系是以天極和春分點作為天球定向基準的坐標系。 為準確表示天體在天球上的投影位置而引入的球面坐標系。根據不同需要,設有地平坐標系,第一赤道坐標系(...
天球坐標系統,是天文學上用來描繪天體在天球上位置的坐標系統。有許多不同的坐標系統都使用球面坐標投影在天球上,類似於使用在地球表面的地理坐標系統。這些坐標...
而因為有天球的概念後,天文學家以此開始創立不同坐標系如黃道坐標系和銀道坐標系。但要注意的是,天球儀是在天球外看天球,天象廳或模擬星象是在天球內看天球...
黃道坐標系是天球坐標系之一。黃道坐標系是以黃道為基圈〔相當於平面直角坐標系的橫軸),以經過春分點的黃經圈(半圓)為始圈(相當於平面直角坐標系的縱軸),以...
地固坐標系也稱地球坐標系,是固定在地球上與地球一起旋轉的坐標系。如果忽略地球潮汐和板塊運動,地面上點的坐標值在地固坐標系中是固定不變的。對於天球坐標系,...
地平線坐標系,也叫地平坐標系。是根據觀察者所處的地平線為基本面所建立起來的天球坐標系統。即以天頂天緯90度,地平線在天球上的投影為天緯0度,以東方為天...
大地測量坐標系是為大地測量所建立的坐標系,主要有兩種類型:天球坐標系,衛星測量把坐標系原點設在地球質心,在天文學中選在日心;地球坐標系,固定在地球上並和地球...
以地球質心為原點,以指向瞬時天極為Z軸,以指向位於瞬時赤道上某一假想的春分點為X軸的右手笛卡兒直角天球坐標系。 套用學科 測繪學(一級學科),大地測量學(二級...
銀道坐標系,是以太陽為中心,並且以銀河系明顯排列群星的平面為基準的天球坐標系統,它的“赤道”是銀河平面。相似於地理坐標,銀道坐標系的位置也有經度和緯度。...
為確定天球上某一點的位置,在天球上建立的球面坐標系。有兩個基本要素:①基本平面。由天球上某一選定的大圓所確定。大圓稱為基圈,基圈的兩個幾何極之一,...
天體坐標,為確定天球上某一點的位置,在天球上建立的球面坐標系。...... 赤道第二坐標系黃道坐標系銀道坐標系為確定天球上某一點的位置,在天球上建立的球面坐...
赤經是天文學使用在天球赤道坐標系統內的坐標值之一,通過天球兩極並與天赤道垂直,另一個坐標值是赤緯。赤經類似於地球經度的角距離。和赤緯一起用來確定天體在天...
球面天文學的具體研究內容一般包括:①天球坐標系的建立,天體的視運動;②視差、大氣折射和光行差的理論及其套用;③歲差和章動對天體位置的影響;④以地球自轉和公轉...
