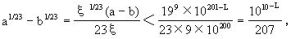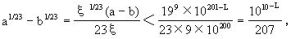天才與鍛鍊

《天才與鍛鍊》作者為華羅庚，於1982年1月發表於《環球》。

基本介紹

• 中文名：《天才與鍛鍊》
• 作者：華羅庚
• 發表日期：1982年1月
• 發表處：《環球》

全文

天才與鍛鍊——從沙昆塔拉快速計算所想到的轟動聽聞的訊息

提問者寫下一個201位的數：

916，748，679，200，391，580，986，609，275，853，801，624，831，066，801，443，086，

224，071，265，164，279，346，570，408，670，965，932，792，057，674，808，067，900，

227，830，163，549，248，523，803，357，453，169，351，119，035，965，775，473，400，

756，816，883，056，208，210，161，291，328，455，648，057，801，588，067，711

解答者馬上回答：這數的23次方根等於9位數546，372，891。

《環球》雜誌的一篇文章中是這樣說的(請參閱《環球》1982年第3期《勝過電子計算機的人》一文)：印度有一位37歲的婦女沙昆塔拉在計算這道題時速度超過了一台最先進的電子計算機。這台在美國得過獎的最現代化、最尖端的產品Univac1180型電子計算機在算這道題時，要先饋入近2萬個指令和數字單元，然後才能開始計算。它整整用了一分鐘時間才算出結果。而沙昆塔拉在教授在黑板上用了4分鐘寫出這個201位數後，僅用50秒鐘就算出了以上的答案。美國報紙稱她為數學魔術師，轟動一時!文章末尾還神秘地說，在她快生孩子的一個星期，她的計算能力出了問題。

面對這樣的問題怎么辦?

看到上述訊息，可能有以下幾種態度：一是驚嘆，望塵莫及，欽佩之至，欽佩之餘也就罷了。二是不屑一顧，我是高等數學專家，豈能為這些區區計算而浪費精力。三是我掌握著快速電子計算機，軟體有千千萬，她一次勝了我算個啥!老實說，有上述這些思想是會妨礙進步的。第一種態度是沒出息，不想和高手較量較量。第二種態度是自命不凡。實際上連計算也怕的人，能在高等數學上成為權威嗎?即使能成，也是“下筆雖有千言，胸中實無一策”，瞧不起套用，又對套用一無所能的人。第三種是固步自封，不想做機器的主人。動腦筋是推進科學發展的動力之一，而勤奮、有機會就鍛鍊是增長我們能耐的好方法。人壽幾何!我並不是說碰到所有的問題都想，而是說要經常動腦筋，來考驗自己。

在我們見到這問題的時候，首先發現文章中答數的倒數第二位錯了，其次我們用普通的計算器(Sharp506)可以在20秒內給出答數。那位教授在黑板上寫下那個201位數用了4分鐘，實際上在他寫出8個數字後，我們就可算出答數了。所以說，沙昆塔拉以50″對1′勝了Univac1180，而我們用Sharp506小計算器以-3′40″勝了沙昆塔拉的50″。但我們所靠的不是天才，而是普通人都能學會的方法。讓我從頭說起吧!

從開立方說起

文章中提到，沙昆塔拉在計算開方時，經常能糾正人們提出的問題，指出題目出錯了，可見他們是共同約定開方是開得盡的。現在我們也做這樣的約定，即開方的答數都是整數。

我國有一位少年，能在一分鐘內開6位數的立方。少年能想得出這個方法是值得稱道的，但美中不足之處在於他沒有把方法講出來，因而搞得神秘化了。當然也考試了人們，為什麼少年能想得出的方法，一些成年人就想不出來，反而推波助瀾造成過分的宣揚?

這問題對我是一個偶遇：在飛機上我的一位助手借了鄰座一位香港同胞的雜誌看，我從旁看到一個數59,319，希望求這數的立方根。我脫口而出答數是39。他問為什麼，我說，前二位不是說明答數的首位是3嗎?尾數是9不是說明答數的末位應當是9嗎?因此答數不該是39嗎?

然後，我告訴他，我的完整想法是：把六位數開立方，從前三位決定答數的第一位，答數的第二位根據原數的末位而定：2、8互換，3、7互換，其它照舊(這是因為1、2、3、4、5、6、7、8、9立方的末位分別為1、8、7、4、5、6、3、2、9)。例如314,432的立方根是68，前三位決定6，末位是2，它決定答數的末位是8。

沙昆塔拉可以脫口而出地回答188,132,517的立方根是573。當然188決定了首位5，末位7決定了3，但讀者試想一下，中間的7怎樣算?

歸納起來可以看出有兩個方法：一個由頭到尾，一個由尾到頭。

習題：求90，224，199的五次方根。

我們怎樣看出答數倒數第二位是錯的

這一點比較難些，要運用一個結果：即a23的最後兩位數和a3的最後兩位數是完全相同的。

913的最後兩位數是71而不是11，而713的最後兩位數才是11，因此答數中的9應當改為7。先不管出現這個差錯的原因是什麼，我們這裡已經做了一個很好的習題。想不到竟是Univac1180把題目出錯了，這事我們後面再講它。

附記我們來證明a23的最後兩位數和a3的最後兩位數相同。當a=2或5時，容易直接驗算。今假定a不能被2和5除盡，我們只要證明a20的末兩位是01就夠了。首先因a是奇數，a2-1總能被8除盡，所以a20-1當然也能被8除盡。其次，因

a4-1=(a-1)(a+1)[(a-2)(a+2)+5]，

a不是5的倍數，所以a-2，a-1，a+1，a+2中肯定有一個是5的倍數。即b=a4-1是5的倍數，而

a20-1=(b+1)5-1=b5+5b4+10b3+10b2+5b.

因而a20-1是25的倍數。從而a20-1是100的倍數。具備些數論知識的人也可從費爾馬定理推出來。

我們怎樣算

我們用的原則是：如果解答是L位整數，我們只要用前L位(有時只要L-1位)或後L位就夠了.用後L位的方法見附錄二，先說前一方法。以前面提到的188,132,517開立方為例，在計算器上算出

公式

就可以看出答案是5.73。

當那位教授說要開201位數的23方時，以23除201餘17，就能預測答數是9位數。當教授寫到第六、七位時，我們就在Sharp506上按這六位和七位數，乘以1016，然後按開方鈕算出

(9.16748×1016)1/23=5.46372873，

(9.167486×1016)1/23=5.46372892，

這樣我們定出了答數的前七位：5,463,728，後二位已由上節的方法決定了，因此答數應該是546,372,871。其實，更進一步考慮，只需利用這個201位數的前八位數字就能在計算器上得到它的23次方根(證明見下面的附記)：

共

但不幸的是，把這個數乘23次方，結果與原來給的數不相符(見附錄一)。與原題比較，發現原題不但尾巴錯了，而且在第八和第九位之間少了一個6。竟想不到Univac1180把題目出錯了，也許是出題的人故意這樣做的。為什麼沙昆塔拉這次沒能發現這個錯誤?看來她可能也是根據前八位算出了結果，而沒對解答進行驗算。

我們的習題沒有白做，答數錯了我們發現了，連題目出錯了我們也糾正了。

結論是：在教授寫到91，674，867時，我們在計算器上按上這八個數字。再乘1016，然後按鈕開23方就可算出答案，總共約用20″就夠了，也就是比那個教授寫完這個數還要快3分40秒，比沙昆塔拉快了4分半鐘。

既然已經知道答數是九位數，或者說在要求答數有九位有效數字時，我們就只需把前八位或九位數字輸入計算機就夠了，而無需把201位數全部輸入機器，進行一些多餘的計算。

附記以a表示那個201位數，b也表示一個201位數，它的前L位與a相同，後面各位都是零。由中值公式，可知存在一個ξ(b<ξ

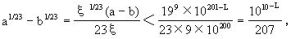
公式

當取L=8時，上式小於1/2，由b1/23的前九位(第十位四捨五入)就可給出a1/23。

虛構

下面講一個虛構的故事，在沙昆塔拉計算表演後，有一天教授要給學生們出一道計算題。一位助手取來了題目。是一個871位數開97方，要求答案有9位有效數字。教授開始在黑板上抄這個數：456，378，192，765，431，892，634，578，932，246，653，811，594，667，891，992，354……當抄到二百多位後，教授的手已經發酸了。“唉!”他嘆了一口氣，把舉著的手放下甩了一下。這時一位學生噗嗤一聲笑了起來，對教授說，當您寫出八位數字後，我已把答案算出來了，它是588，415，036.那位助手也跟著笑了。他說，本來後面這些數字是隨便寫的，它們並不影響答數。這時教授恍然大悟，“哈哈，我常給你們講有效數字，現在我卻把這個概念忘了。”

多餘的話

我不否認沙昆塔拉這樣的計算才能。對我來說，不要說運算了，就是記憶一個六、七位數都記不住。但我總覺得多講科學化比多講神秘化好些，科學化的東西學得會，神秘化的東西學不會，故意神秘化就更不好了。有時傳播神秘化的東西比傳播科學更容易些。在科學落後的地方，一些簡單的問題就能迷惑人。在科學進步的地方，一些較複雜的問題也能迷惑人。看看沙昆塔拉能在一個科學發達的國家引起轟動，就知道我們該多么警惕了，該多么珍視在實踐中考驗過的科學成果了，該多么慎重地對待一些未到實踐中去過而誇誇其談的科學能人了。

同時也可以看到，手中拿了最先進的科學工具，由於疏忽或漫不經心而造成的教訓。現代計算工具能計算得很快很準，但也有一個缺點，一旦算錯了，不容易檢查出來。對於計算象201位數字開23次方這類的問題——多少屬於數學遊戲性質的問題，算錯了無所謂，而對在實際運用中的問題算錯了就不是玩的。“二萬條指令”出錯的可能性多了，而在演算過程中想法少用或不用計算機演算，檢查起來就不那么難了。這說明人應該是機器的主人，而不是機器的奴隸。至於大算一陣嚇唬人的情況就更不值一提了。這裡我們還可以看到基本功訓練的重要性。如果基本功較差，那么就是使用大型計算機來演算201位數開23次方也要1分多鐘才能算完。而有了很好的基本功，就是用小計算器也能花比1分鐘少的時間算出來。

這是一篇可寫可不寫的文章，我之所以寫出的原因，在於我從沙昆塔拉這件事中得到了啟發，受到教育，我想，這些也許對旁人也會是有用的。

發表

華羅庚《天才與鍛鍊》全文，原文於1982年1月發表於《環球》。