大系統分散隨機控制(large-scale system de- centralized stochastic co ntrol)具有隨機干擾的大系統控制問題。
基本簡介,數學模型,
基本簡介
大系統分散隨機控制(large-scale system de- centralized stochastic co ntrol)具有隨機干擾的大系統控制問題。它包括基於分散化量測、估計而進行的分散控制和隨機最佳化.以離散時間情形為例。
數學模型
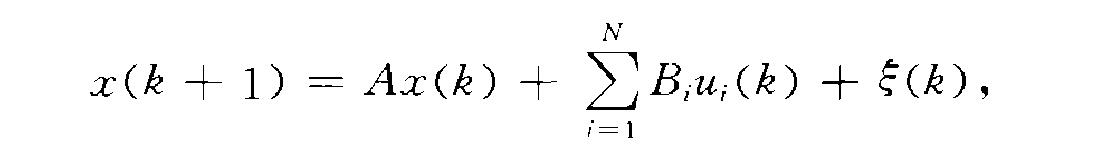
其中二為n維狀態向量,u;(k)是第i控制站k時刻的m維控制;S(k)為零均值、方差為V (k)的白噪聲序列;控制站i的量測結果為yr(k)=C;x(k)+ }j, ( k,噪聲rj; ( k)亦設為零均值、方差為W; (k)的白噪聲序列;其最優控制問題為:求分散控制作用 <u;<k)(i=1,2,""",N,k=1,2,""",Ii),使下列費用函式極小化:
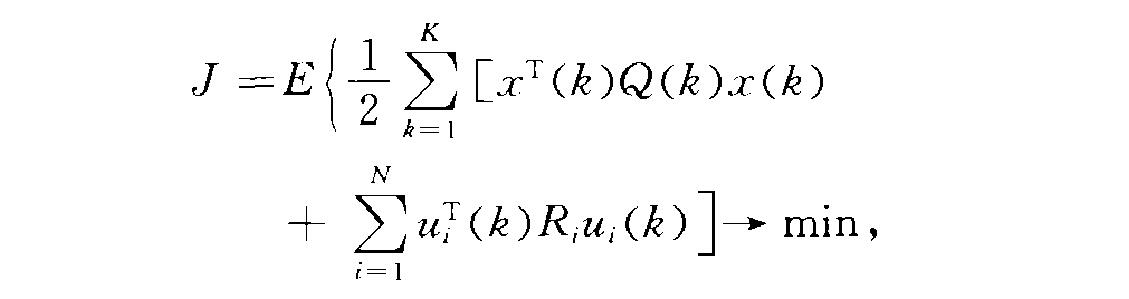
其中Q(k),R均為適當維數的正定矩陣. 這一問題的求解與系統的信息結構有密切的關係.常見的信息結構包括:具有完全信息的“非分散解”,控制站之間具通信延遲的“一步延遲共享信息結構”等.威騰豪森(Witsenhausen , S.)曾舉出一個非古典信息結構的反例表明其不可解性,它又與多人組隊決策問題有密切的關係(參見“組隊決策”).
