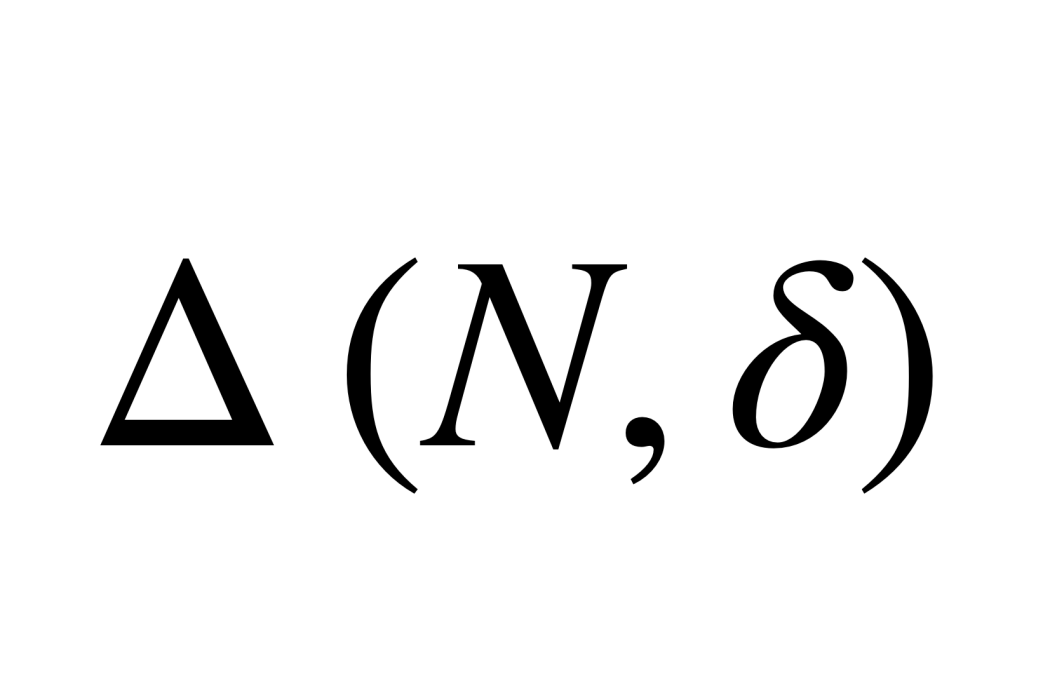大篩法由林尼克於1941年提出，並用於研究模素數的最小二次非剩餘估計。1947年，雷尼對大篩法作了重要改進與發展，並將它用於等差數列中素數分布的中值公式及哥徳巴赫猜想。
基本介紹
- 中文名：大篩法
- 外文名：large sieve
- 適用範圍：數理科學
- 定義：研究模素數的最小二次非剩餘估計
歷史,套用,
歷史
大篩法是近代解析數論的一個重要工具。
為了研究模p的最小正的二次非剩餘，林尼克於1941年首次提出了大篩法。
1948年，雷尼對大篩法做了重要改進，用來研究算術級數中素數的平均分布，並結合布龍篩法證明了結論{1,n}：每個充分大的偶數均可表為一個素數和一個至多有n個素因子的殆素數之和。這一結果顯示了大篩法的強大威力，但初期的大篩法表述比較麻煩，其實質不易為人理解。
1965年，羅思(Roth, K. F.)與邦別里(Bombieri, E.)先後對大篩法做了重要改進。特別是邦別里的工作，把大篩法建立在一個便於使用的分析形式上，並得到了重要的套用，即證明等差數列中素數分布的中值公式。
此後，達文波特(Davenport, H.)與哈伯斯塔姆(Halberstam,H.)又明確給出大篩法的分析形式，這就是人們普遍採用作為定義的大篩法形式。從此，大篩法不斷得到深人的研究，在解析數論的一系列著名問題的研究中發揮了重要的作用。
套用
普通的篩法是這樣的：
有一個有限集合A及一個有限素數集合P，對於
,要求
滿足
，其中r為一個常數，問這種a的個數如何估計？
在原始的大篩法中，r不是常數，它隨p而無界增長，形象地說，大篩法地“篩眼”是“很大的”。
1965年，羅思與邦別里對大篩法作出了重大貢獻。特別是邦別里的工作考試將大篩法建立在一個更合適與方便的分析形式上，並得到了重要的套用，即證明等差數列中素數分布的中值公式。
因此這項工作可以看作大篩法的另一階段，即大篩法就是某種指數和均值估計。
詳言之，命M與N(≥1)為整數，且
為任意複數。命
。又命
且
為
中的一組遞增實數，滿足
。大篩法就是要建立以下形式的不等式：
。其中
僅依賴於N，δ，要求∆儘可能好的估計。
