基本介紹
- 中文名:大數律
- 外文名:law of large numbers
- 別稱:大數定律
- 領域:數學
- 屬性:機率論與數理統計學的一基本定律
- 分類:弱大數律和強大數律
簡介
分類



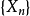
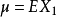
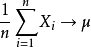
重要的大數律
切比雪夫大數定理



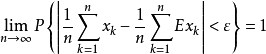
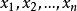
伯努利大數定律
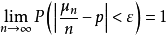
辛欽大數定律

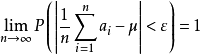




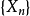
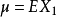
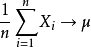


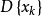

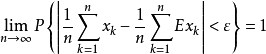
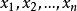
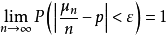

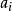
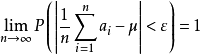
大數律,即大數定律,是機率論中討論隨機變數序列的算術平均值向常數收斂的定律,是機率論與數理統計學的基本定律之一。大數律有弱大數律和強大數律之分。在隨機...
馬爾可夫大數律(Markov law of large num-hers)一種弱大數律.設隨機變數序列y } }z }…滿足條件:對於任意n)l,均有馬爾可夫大數律不僅能用於獨立的隨機變數...
格涅堅科大數律(Gnegenko law of largenum一hers)一種弱大數律.設寧,,寧2,…為隨機變數列若記...
切比雪夫大數律(Chebyshev law of large num-hers)一種弱大數律,設寧1,寧:,…為兩兩不相關的隨機變數序列,它們的方差有限,且有公共的上界,即存在常數‘,...
伯恩斯坦大數律(Bernstein law of large num-bers)一種弱大數律...... 伯恩斯坦大數律(Bernstein law of large num-bers)一種弱大數律.設 …為隨機變數序列,...
泊松大數律(Poisson law of large numbers )一種弱大數律.設產,為n次獨立試驗中某事件A出現的次數,p;(0<p,<l}i -1}2,""",n)為事件A在第i次試驗...
波萊爾強大數律(Borel strong law of largenumbers)關於伯努利試驗的強大數律。...... 波萊爾強大數律(Borel strong law of largenumbers)關於伯努利試驗的強大數律...
柯爾莫哥洛夫強大數律(Kolmogorov strong law of large numbers)是最重要最常用的強大數律。若{Xn}為獨立同分布隨機變數序列,EXn存在,則以機率1成立n個獨立同...
