多面形半群是伴隨多面體的一種代數結構.由多面形錐K={xEE"}Ax>0}中的整點相對於加法而構成的半群KZ.對由整向量組成的半群B。
多面形半群(polyhedral semigroup)伴隨多面體的一種代數結構.由多面形錐K={xEE"}Ax>0}中的整點相對於加法而構成的半群KZ.對由整向量組成的半群B,若其中的每個元素均可表示為已知t()1>個整向量甲,了,…,了的正整數組合,即B一{二…二一藝Z}q' , Z,為正整數,1<j<t}.
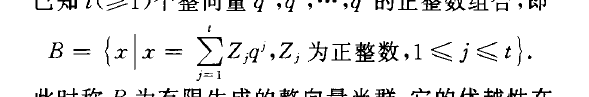
此時稱B為有限生成的整向量半群.它的優越性在於可以同時具有約束方程組形式表示以及有限生成的組合形式表示.因此,對於多面形半群一個重要的問題是研究在什麼樣的條件下,它是有限生成的.當矩陣A的元素為有理數時,多面形半群KZ是有限生成的.
