多面函式1971年哈笛(Hardy)提出。
基本介紹
- 中文名:多面函式
- 提出時間:1971
- 提出人:哈笛(Hardy)提出
- 介紹:多面函式擬合法
簡介,例如,
簡介
1976年將此法套用於美國大地測量、擬合重力異常、大地水準面差距、垂線偏差等,1978年將此法用於地殼形變。它的基本思想是任何一個規則或不規則的連續曲面均可以由若干簡單面(或稱單值數學面)來疊加逼近。具體做法是在每個數據點上建立一個曲面,然後在方向上將各個旋轉曲面按一定比例疊加成一張整體的連續曲面,使之嚴格地通過各個數據點。
多面疊加的數學表達式為:
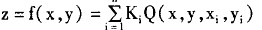
這裡Q(X,Y,Xi,Yi)為參加插值計算的簡單數學面,又稱為多面函式的核函式;n為簡單數學面的張數或多層疊加面的層數,它的值與分塊擴充範圍內參與點的個數相等;Ki(i=1,2,3,4,n)為待定參數,它代表了第i個核函式對多層疊加面的貢獻。為了計算方便,多層疊加面中的n個核函式一般選用同一類型的簡單函式,通常是圍繞豎向軸旋轉的曲面,這條豎正好通過某一參考點,
例如
:
(1)錐面
Q1(x,y,xi,yi)=C+[(x—xi)^2 +(y—yi)^2]^0.5
(2)正雙曲面
Q2(x,y,xi,yi)=[(x—xi)^2 +(x—xi)^2+a]^0.5
(3)倒雙曲面
Q3(x,y,xi,yi)=[(x—xi)^2 +(y—yi)^2+a]^-0.5
(4)三次曲面
Q4(x,y,xi,yi)=[(x—xi)^2 +(y—yi)^2+a]^-1.5
當己知數m大於節點數n時,利用最小二乘法原理,計算方程係數.在核函式權陣的情況下,也可以計算方程係數。係數求出後,同樣可以求出待求點的∈,從而求出H 。
