基本介紹
- 中文名：多貝西小波
- 外文名：Daubechies Wavelet
- 本質：一種小波函式
- 命名人：Ingrid Daubechies
簡介,性質,建立,
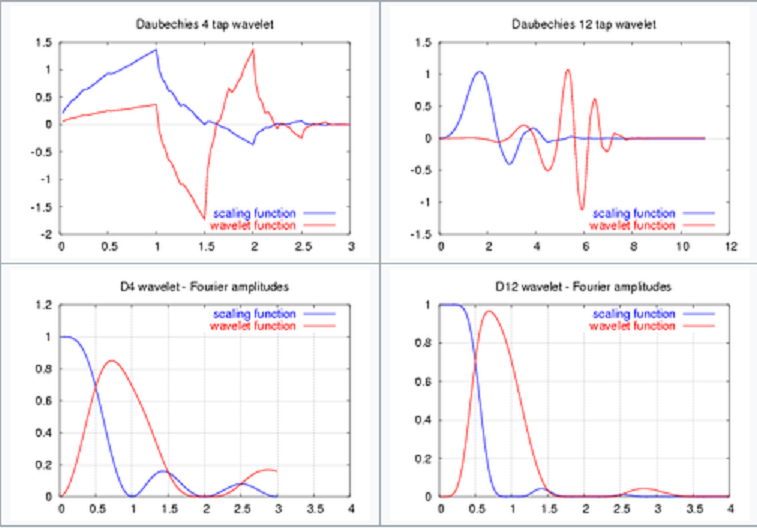
簡介
一般而言的離散小波轉換通常是以正交小波（orthogonal wavelet）為基底，而多貝西小波也是一種正交小波。由於它很容易經由快速小波轉換（fast wavelet transform（FWT））實現，所以常會放在數位信號處理的教科書中教學。
對於有限長度的小波，套用於快速小波轉換（fast wavelet transform（FWT））時，會有兩個實數組成的數列：一是作為高通濾波器的係數，稱作小波濾波器（wavelet filter,也稱為mother wavelet）；二是低通濾波器的係數，稱作調整濾波器（scaling filter,也稱為father wavelet）。
我們則以濾波器的長度N來形容濾波器為DN，例如：N=2的多貝西小波寫作D2、N=4的多貝西小波寫作D4，以此類推（N為偶數）。實際上常用的多貝西小波為D2到D20。
性質
分類方式
- 多貝西小波的分類是以消失動量（vanishing moment）的值A（亦為消失動量的個數）為依據（A稱為tap），調整函式（scaling function）及小波函式（wavelet function）的平滑度（smoothness）皆會隨著消失動量的值（tap）增加而增加：例如，當A=1時，多貝西小波即是哈爾小波（Haar wavelet），調整函式及小波函式都是不連續的；當A=2時，多貝西小波的調整函式及小波函式為不能平滑微分的連續函式；當A=3時，調整函式及小波函式已經是連續可微的函式了。以此類推，當A愈大時，多貝西小波的兩個函式平滑度會愈來愈高。
長度
- 多貝西小波的長度為消失動量（vanishing moment）值A的兩倍；所以當消失動量為A時，多貝西小波的小波濾波器（wavelet filter）及調整濾波器（scaling filter）長度皆為2A（N=2A）。一般而言，我們仍是以N來形容多貝西小波的長度：例如，當A=1時，有一個消失動量，多貝西小波寫成D2，長度為2（也是Haar小波）；當A=2時，有兩個消失動量，多貝西小波寫成D4，長度為4；以此類推。但是，在matlab的使用上是以dbA描述多貝西小波，以下則為調整濾波器的係數及A的關係：
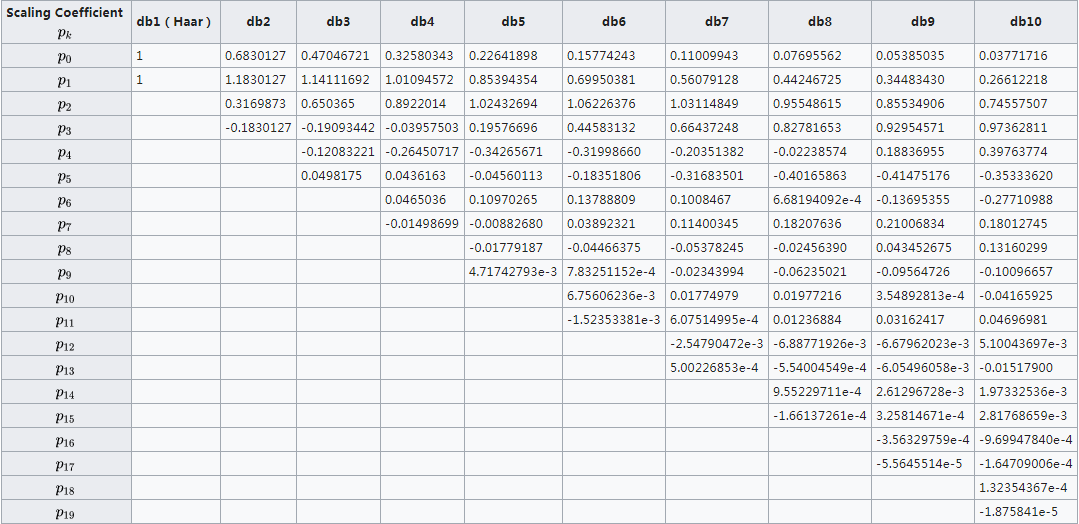
正交多貝西小波係數
建立
多貝西小波具有調整函式（低通濾波）及小波函式（高通濾波）兩個函式。因此，我們需先建立調整函式及小波函式的係數:
首先，調整函式在多尺度分析（multi-resolution analysis）中的每一層皆可寫為下列方程式：
其中
亦為有限長度的實數數列，稱做小波係數。
因為上述方程式必須是齊性的（homogeneous），在建立上，這兩個函式會正規化（normalize）為和（sum）及平方和（sum of square）皆是2。
正交小波
正交性質在此指調整係數就必須和位移偶數間隔後的調整係數互相垂直（內積為0），即為下式：
由於正交的特性，小波係數會滿足下列條件：
消失動量及多項式估計
常用的多貝西小波為D2到D20，由於多貝西小波的消失動量為有限個，所以調整及小波係數可以表示為有限長度的多項式
上式經過Z轉換（Z-transform）後會變成：
我們可以將上式轉換為正交離散小波轉換的一般表示式
而正交的條件可寫成
因此
便成為對稱型勞倫滋多項式，即。因為
及
, 
則會是區段[0,2]中的非負實數。
方程式（#）如果除上的truncated power series則可求得對於每個
的最小解
而（#）的齊性方程式是一個對於
的反對稱方程式，因此可得一般解為
，此一般解有
個多項式實係數。
因此和為
(sum)
為了解出
的
，這裡使用Fejer-Riesz-algorithm這個方法（此為頻譜分解的方法）。多項式會因此分開成許多線性因子（linear factor）
,此時
。每一個線性因子代表可以分解成兩個線性因子的一個勞倫茲多項式
，任選其中一個線性因子都可設為
。所以會有2個可能的答案。為了極端相位的目的，挑選所有根都是在單位圓上或是在單位圓內複數根的。
