多模型控制在解決非線性及各種複雜系統控制問題中己經得到深入研究,並在飛行器控制、故障診斷、化學化工等許多領域得到廣泛的套用。多個模型之間的切換次序、切換過程的穩定性、模型的數量是設計多模型切換控制系統的關鍵。
基本介紹
- 中文名:多模型切換控制
- 外文名:Multi-model switching control
- 學科:控制科學與工程
- 思想提出:Martensson
- 切換方法:直接切換、間接切換
- 套用:飛行器控制、故障診斷
基本概念,基本思想,結構,模型切換性能指標,二次型性能指標,ITAE性能指標,積分型性能指標,1-範數性能指標,
基本概念
多模型控制器於70年代被提出,主要用於解決參數不確定系統的控制問題。主要是對被控對象建立多個模型,覆蓋其參數不確定性,利用輸出誤差求取加權值,然後通過加權求和的形式求取控制器,但其穩定性很難證明。多模型控制在解決非線性及各種複雜系統控制問題中己經得到深入研究,並在飛行器控制、故障診斷、化學化工等許多領域得到廣泛的套用。多個模型之間的切換次序、切換過程的穩定性、模型的數量是設計多模型切換控制系統的關鍵。
基本思想
切換的思想首先由Martensson提出,主要有兩種切換方法:
第一種是直接切換,首先根據被控對象的參數不確定性建立多個控制器,下一個控制器的選擇是預先知道,基於切換函式逐一切換,直到穩定的控制器,滑模變結構控制就是這一類切換。
第二種方法是間接切換,每一採樣時刻根據性能指標切換函式值選擇與實際被控對象最接近的模型,並將基於此模型的控制器切換為當前控制器。本文主要論述這種方法。
因為在一段時間內僅有一個控制輸入,任何控制器性能只有在使用才能計算,而辨識模型的性能是每一步並行計算,因而性能指標必須基於模型性能而不是控制器的性能。在實際運行中,通過性能指標判斷模型集中那個模型與被控對象最為接近。通過開關切換至該模型對應的控制器中。
結構
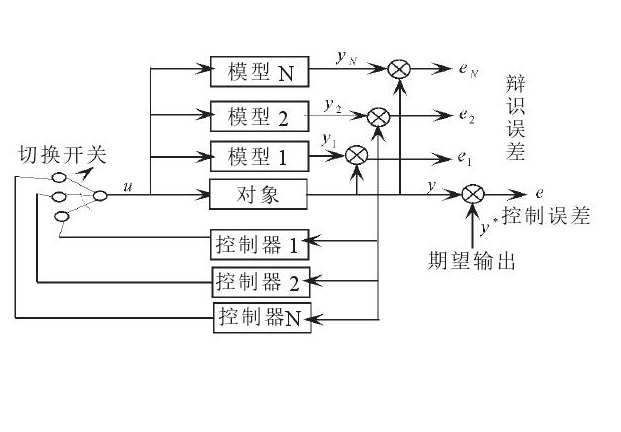
基於切換的多模型控制結構如下:
圖1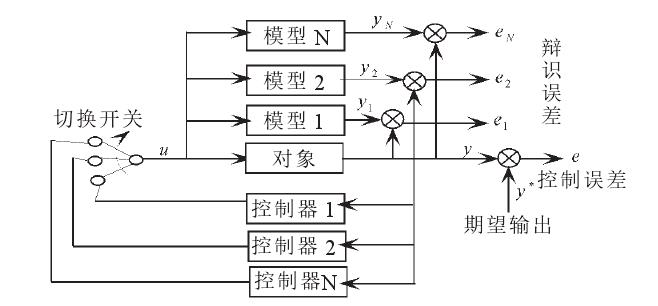

基於多模型的智慧型控制方法是通過在s個局部控制器之間切換來實現。根據多個不同模型的翰出,依據切換控制策略來適應被控對象的參數突變,同時保證了閉環系統的穩定性和輸出跟蹤誤差的漸近收斂性。
模型切換性能指標
切換性能指標在多模型自適應控制中是用來判斷和選擇最佳模型及相應的控制器,因此性能指標要能夠最準確地反映過程與模型的匹配程度。
首先,我們可以從對象最佳化的角度看,選擇恰當的性能指標。
二次型性能指標
基於跟蹤調節的二次型性能指標:
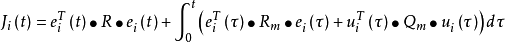
性能指標選取的是實時誤差和歷史誤差的加權,歷史誤差數據是“無限記憶”,從最優的角度衡量模型與被控對象的匹配程度。與傳統線性二次調節器的區別在於這個最優性能指標不是用來設計控制器,而是用來衡量模型與對象的接近程度,其中誤差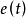 為辨識誤差。
為辨識誤差。
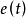
ITAE性能指標
基於ITAE準則的性能指標(或基於ITAE準則的性能指標):

在以上兩種性能指標中包含兩項:時間t和辨識誤差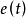 。其中辨識誤差
。其中辨識誤差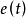 反映了辨識模型與實際對象的匹配程度,時間t保證系統快速穩定的切換至最佳模型。
反映了辨識模型與實際對象的匹配程度,時間t保證系統快速穩定的切換至最佳模型。
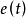
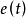
其次,基於真實值與模型值的接近程度的思想,提出切換性能指標作為某種距離的度量。
積分型性能指標
由Yale大學的Narendra首先提出一種積分型性能指標:

其中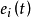 為第i個辨識模型與實際對象的誤差,
為第i個辨識模型與實際對象的誤差,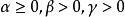 ;
;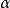 和
和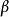 分別為暫態內和記憶長度的加權因子,側重於性能指標的實時和長期匹配程度,
分別為暫態內和記憶長度的加權因子,側重於性能指標的實時和長期匹配程度,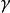 為遺忘因子,它決定了指標存儲能力和保證
為遺忘因子,它決定了指標存儲能力和保證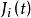 的收斂性,合理的選擇入可以獲得很好的性能指標。
的收斂性,合理的選擇入可以獲得很好的性能指標。
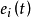
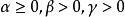
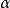
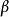
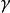
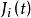
1-範數性能指標
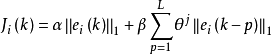
其中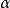 >0為現在時刻誤差的權重,
>0為現在時刻誤差的權重,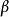 >0為過去時刻誤差組合的權重,
>0為過去時刻誤差組合的權重,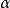 和
和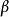 數值確定現在時刻誤差和過去時刻。
數值確定現在時刻誤差和過去時刻。
誤差組合對性能指標的相對重要程度,遺忘因子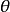 表示性能指標的記憶效果,L為所取的過去時刻誤差組合的長度。遺忘因子的合理選擇可以部分消除初始狀態偏差,外部干擾等因素的影響。
表示性能指標的記憶效果,L為所取的過去時刻誤差組合的長度。遺忘因子的合理選擇可以部分消除初始狀態偏差,外部干擾等因素的影響。 為1一範數。同理,也可以選取任意範數作為性能指標。
為1一範數。同理,也可以選取任意範數作為性能指標。
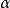
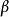
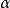
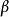
誤差組合對性能指標的相對重要程度,遺忘因子