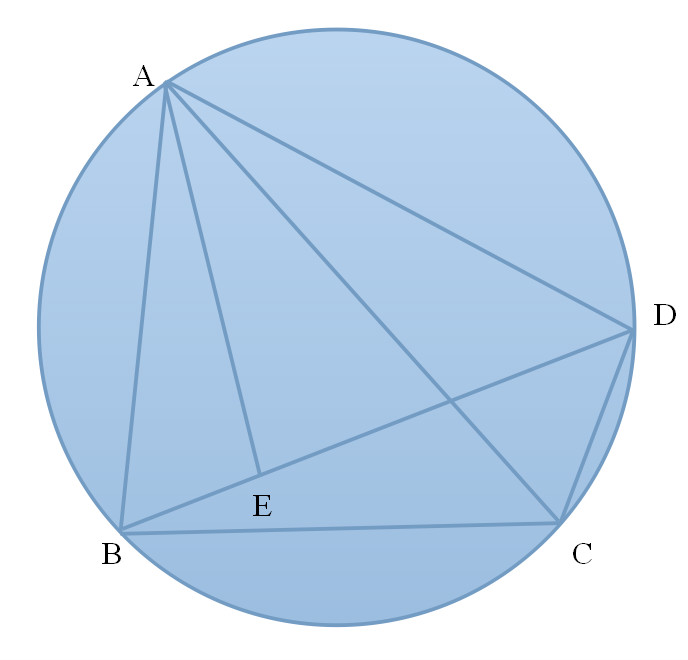
命題內容:圓內接四邊形對角線的乘積等於兩對邊乘積之和。
即:AC*BD=AD*BC+AB*CD .
多列米定理實際上就是托勒密定理。
基本介紹
- 中文名:多列米定理
介紹,相關信息,
介紹
圓內接四邊形對角線的乘積等於兩對邊乘積之和,即托勒密定理在圓中的特殊情況
在四邊形ABCD中,連線AC,作角BAE=角CAD,角ABE=角ACD
則三角形ABE和三角形ACD相似
所以 BE/CD=AB/AC,即BE*AC=AB*CD (1)
又有比例式AB/AC=AE/AD
而角BAC=角DAE
所以三角形ABC和三角形AED相似.
BC/ED=AC/AD即ED*AC=BC*AD (2)
(1)+(2),得
AC(BE+ED)=AB*CE+AD*BC
又因為BE+ED>=BD
所以命題得證
註:多列米定理實際上就是托勒密定理。
托勒密(Ptolemaeus,Claudius;Ptolemy),古希臘地理學家、天文學家、數學家。
相關信息
在RtΔABC中,設直角邊BC = a,AC = b,斜邊AB = c(如圖). 過點A作AD∥CB,過點B作BD∥CA,則ACBD為矩形,矩形ACBD內接於一個圓. 根據多列米定理,圓內接四邊形對角線的乘積等於兩對邊乘積之和,有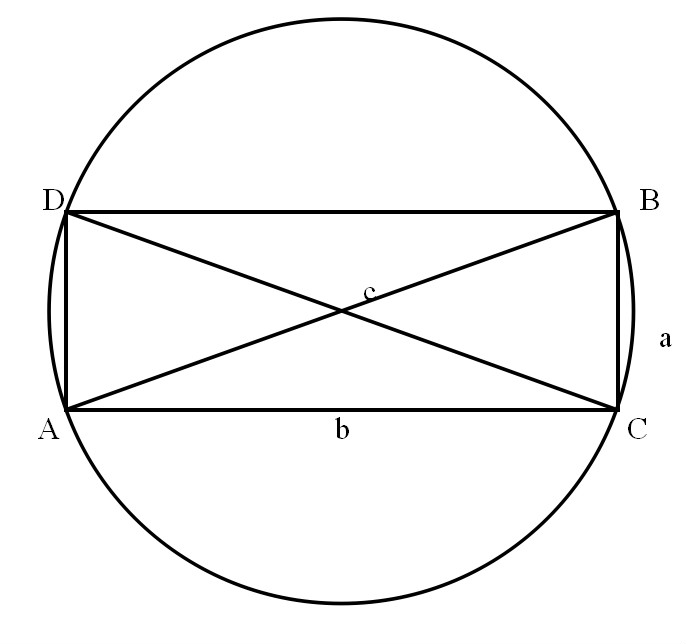

AC*BD=AD*BC+AB*CD,
∵ AB = DC = c,AD = BC = a,AC = BD = b,
∴ AB^2=BC^2+AC^2,即 a^2+b^2=c^2