外爾本原代數(Weyl primitive algebra)是一種特殊的本原代數。
定義
外爾(Weyl, H.)給出的一個本原代數的例子.若F {.x1,二:,…,二,}y}}yz,...,y}是特徵為零的域F上2n個元素二,,二:,…,二,,y},yz,...,y。的自由代數.了是由
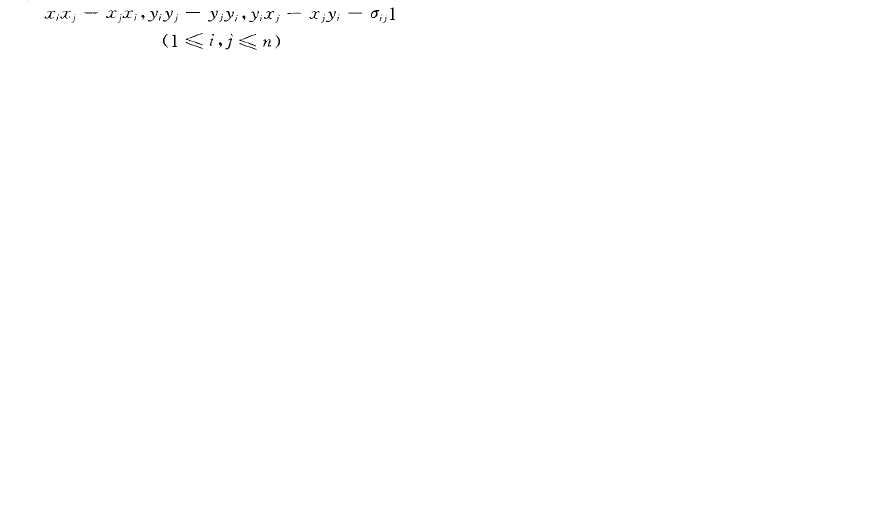
在F{二,,xz,x},y
yz,, y.,}中生成的理想,則
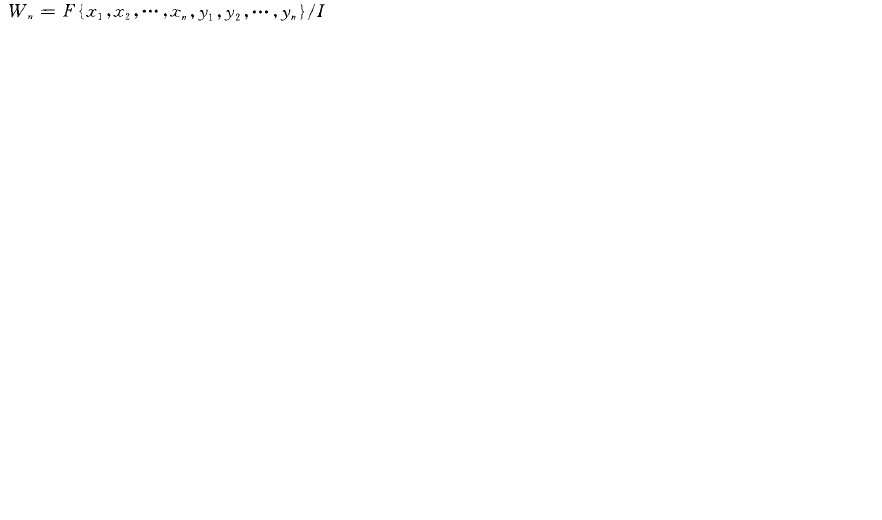
是F'上本原代數,稱為外爾(本原)代數,W,:也為單代數.外爾代數也是微分運算元環的基本例子之一W。作為位置和動量運算元所生成的代數首先出現在量子力學中,生成元的不可換性反映了海森堡不定ly原理.
