外伸梁:一端或兩端伸出支座外的簡支梁。
外伸梁的一端或兩端伸出支座之外,外伸梁自由端的撓度,受跨中荷載的影響,跨中荷載足夠大時,外伸梁的自由端會往上翹;懸臂樑自由端的撓度,只與懸臂的線剛度及懸臂樑的荷載有關。
基本介紹
- 中文名:外伸梁(伸臂梁)
- 外文名:Beam with an overhang
- 分類:力學名詞
簡介
變形求解

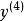

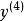
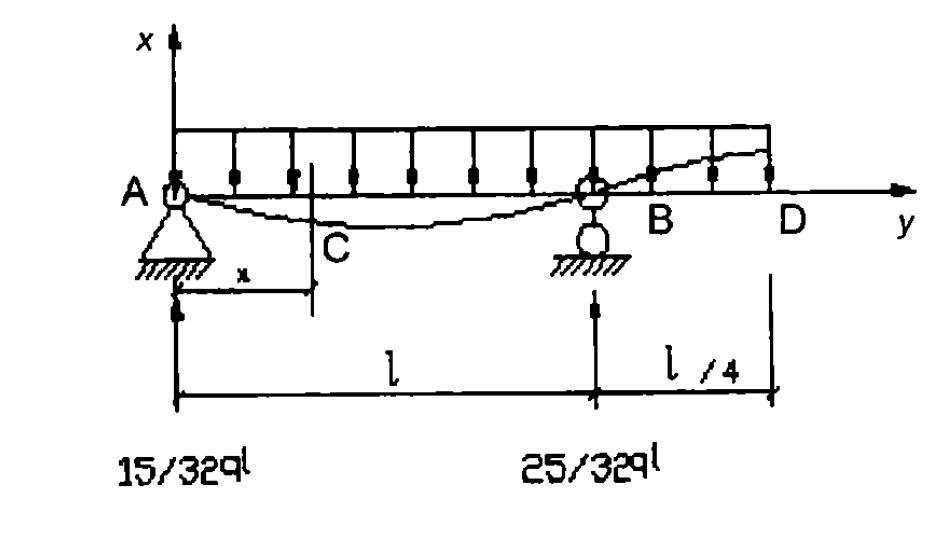 圖1
圖1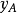



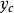
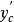
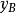

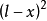

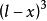
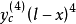








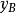
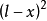




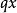
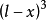

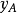
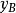
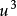
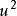
加固混凝土外伸梁
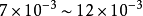

外伸梁:一端或兩端伸出支座外的簡支梁。
外伸梁的一端或兩端伸出支座之外,外伸梁自由端的撓度,受跨中荷載的影響,跨中荷載足夠大時,外伸梁的自由端會往上翹;懸臂樑自由端的撓度,只與懸臂的線剛度及懸臂樑的荷載有關。


 圖1
圖1



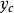
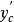
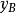

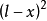

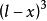
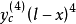



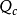




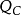

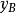
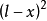




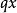
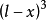

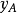
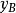
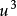
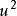
外伸梁:一端或兩端伸出支座外的簡支梁。外伸梁的一端或兩端伸出支座之外,外伸梁自由端的撓度,受跨中荷載的影響,跨中荷載足夠大時,外伸梁的自由端會往上翹;...
根據我們的長期實踐經驗及理論分析,可以套用GB/T1456三點外伸梁彎曲法來測試複合材料層板的G13、G23等。三點外伸梁彎曲法的特點是,可以用梁外伸端的位移(撓度)...
梁分為靜定梁和非靜定梁;靜定梁分為單跨梁和多跨梁;多跨梁又叫組合梁;單跨梁分為懸壁梁,簡支梁,外伸梁;懸壁梁一端固定一端自由;簡支梁兩端都是鉸鏈;外...
現澆鋼筋混凝土結構中,從連續梁端支座延伸出來一定長度的梁段或者直接從柱子連線出來,端部是沒有支承的梁也屬於挑梁,前者稱外伸梁,後者稱懸臂樑。...
4.6 鋼筋混凝土外伸梁設計實例學習指導思考題習題第5章 鋼筋混凝土受壓構件承載力計算5.1 受壓構件的構造要求5.2 軸心受壓構件正截面承載力計算...
9.2 用靜力法作單跨靜定梁的影響線 1729.2.1 簡支梁的影響線 1729.2.2 外伸梁的影響線 1779.3 間接荷載作用下簡支梁的影響線 180...
2.2.6 外伸梁的反力、剪力、彎矩和撓度……第3章 建築結構荷載第4章 建築結構構造第5章 建築結構抗震設計第6章 建築地基基礎...
多吊點起重臂在設計計算時,起昇平面的力學模型為多支點外伸梁,因而是多次超靜定結構的起重臂。特點與雙吊點起重臂相類似,但不常用。...
二、外伸梁的影響線388三、內力圖與內力影響線的區別389第四節機動法繪製多跨靜定梁的影響線389一、機動法的基本原理390二、機動法繪製多跨靜定梁影響線390...
因為迴轉中心偏離在陸側,所以主控制室多半安置在從轉台外伸的樑上,以改善操作者的視線。有時將主控制室安置在一個可以伸縮的外伸梁上,當工作時主控制室外伸,...
第一節 簡支梁、外伸梁、懸臂樑、連續梁、單筋梁、雙筋梁第二節 梁的高跨比及截面尺寸的確定第三節 荷載統計與梁的內力第四節 單筋梁的正截面設計和梁的...
思考題第十三章 梁與柱第一節 簡支梁、外伸梁、懸臂樑、連續梁、單筋梁、雙筋梁第二節 梁的高跨比及截面尺寸的確定第三節 荷載統計與梁的內力...
