在圖論學科中,塔特定理是具有perfect matching的圖的一個表征。將二部圖的霍爾定理推廣到任意圖。它是Tute-Berge公式的一個特例。
基本介紹
定義
塔特-伯格公式
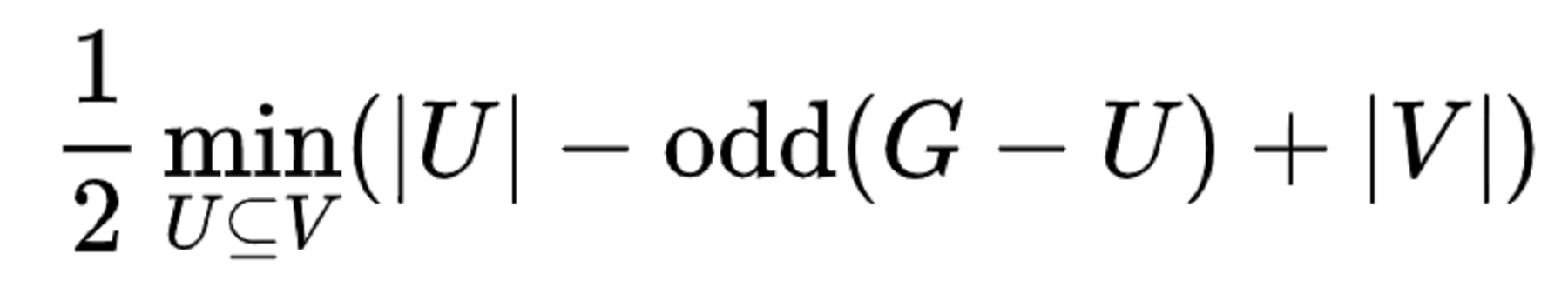
在圖論學科中,塔特定理是具有perfect matching的圖的一個表征。將二部圖的霍爾定理推廣到任意圖。它是Tute-Berge公式的一個特例。
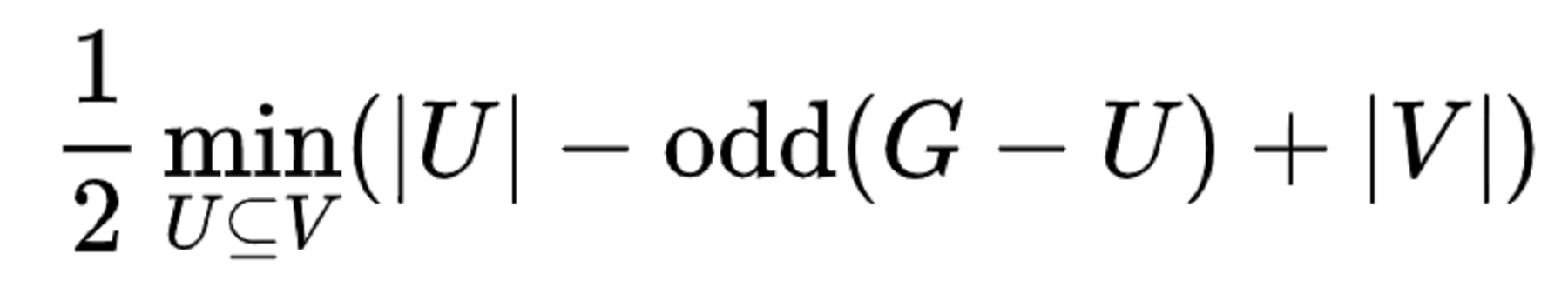
在圖論學科中,塔特定理是具有perfect matching的圖的一個表征。將二部圖的霍爾定理推廣到任意圖。它是Tute-Berge公式的一個特例。定義圖 G=(V,E) 有perfect matching若且唯若滿足 ...
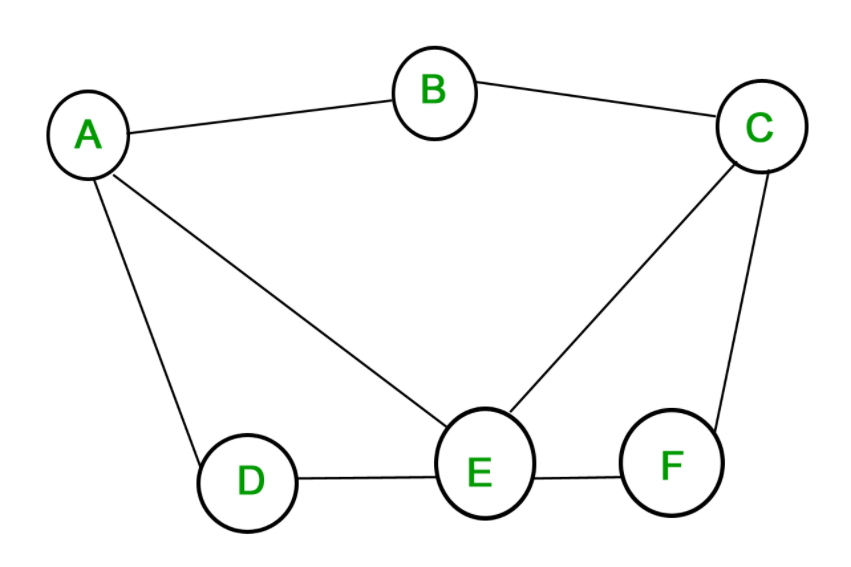
在圖論的數學學科中,塔特-伯格公式是對圖中最大匹配的大小的一個表征。以右圖為例,去掉中心那個頂點會產生三個奇分量(即圖中三個五頂點分量)。因此,根據塔特-伯格公式公式,任何匹配中最多有(1−3+16)/2 = 7條邊。定義 一個圖G=(V,E)的最大匹配的大小等於 其中odd(G-U)表示這個圖當中有多少個...
塔特-格羅騰迪克不變數(Tutte-Grothendieck invariant)是一種度量,指擬陣M上的且滿足如下條件的不變數f:1.當擬陣M₁,M₂同構時,f(M₁)=f(M₂).2.若M為M₁,M₂的直接和,即M=M₁⊕M₂,則f(M)=f(M₁)f(M₂).3.當M的元素e不是自環,或單點割集時,f(M)=f(M-e)+f(...
其中他所提出的著名的塔特猜想,於1983年由法爾廷斯所證明。70年代,他的研究重點是代數K理論,研究它與伽羅瓦上同調的關係。同時開闢“剛性解析空間”這一研究方向,他在橢圓曲線及模函式這一與費馬大定理有關方面的論著是經典的。對其中至關重要的伯奇—斯溫耐頓—代爾猜想進行了細緻研究。80年代,他重點研究斯塔克...
定理 𝐾, 𝐶, 𝑃含完美匹配。塔特定理:圖 G=(V,E) 有完美匹配若且唯若滿足 ∀U⊆V,o(G−U)≤|U|,o(X) 表示 X 子圖的奇連通塊數。Peterson定理:每一個無橋的、3-正則圖都含有一個完美匹配。若一個含2n個點的圖G滿足最小度δ(G)≥n,則G含一個完美匹配。
定理1設圖G在單元集 之下的邊覆蓋多項式為P(G),並設 為G的一個偽子圖,則 其中 為G關於H的一切極大的部分邊覆蓋的集合。點覆蓋多項式的消去定理 取定圖G的一個偽子圖 ,考察由它除去一些邊所成的偽子圖H的集合 對於每一個 ,又考察部分點覆蓋的集合 {部分點覆蓋 }. (4)就是G關於H的部分點覆蓋,...
阿廷在他與J.T.塔特合寫的類域論(1951~1952)的講稿中提出了類結構的概念,將局部的和整體的、數域的和代數函式域的類域論納入同一個公理化體系中。基本定理 主定理 任意的相對Abel域K/k是k的某個理想群的類域。存在定理 對於任意的理想群H(m),存在H(m)的類域。合成定理 設K₁,K₂為H₁,H₂...
但該系統卻推出了兩個定理①Op→p,解釋為:如果應當p,則p是事實上真的;②Op凮p,解釋為:應當p,若且唯若p是事實上真的。這些定理背離了“應當”這一道義概念的含義,並導致道義邏輯等值於通常的命題邏輯。30年代A.霍夫斯塔特、J.C.C.麥肯舍、K.格耐里等人發表的幾篇關於道義邏輯的論文,也有類似於馬利提出...
另一方面,自1940年以來,生於英國的塔特(Tutte,W.T.)在解決拼方問題中取得了一系列有關圖論的結果,這些不僅開闢了現今圖論發展的許多新研究領域,而且對於20世紀30年代,惠特尼(Whitney,H.)提出的擬陣論以及人們稱之為組合幾何的發展都起到了核心的推動作用。應該特別提到的是在這一時期,隨著電子技術和...
泰特猜想(Tait's conjecture)是關於圖的著色的一個著名猜想,3正則圖的3邊正常著色稱為泰特著色。泰特猜想:每個簡單3正則3連通平面圖都有泰特著色,它與四色猜想等價,泰特(P.G.Tait)曾根據“每個3正則3連通平面圖都是哈密頓圖”的錯誤假設,給出了四色猜想的一個“證明”,塔特(W.T.Tutte)於1946年構造...
