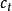1941年馬丁和辛格建立的“塔板理論”模型將色譜柱看作一個分餾塔,構想其中均勻分布許多塔板,並認為在每個塔板的間隔空間內,組分在兩相中立即達到分配平衡,經過多次的分配平衡後,分配係數小的組分先流出色譜柱,並得到描述色譜流出曲線的表達式。同時塔板理論還引人理論塔板數(plate ntlIllber of theoretit·al plates)和理論塔板高度(plate height)作為衡量色譜柱效的指標。
基本介紹
簡介,內容,基本假設,結論與意義,
簡介
馬丁(Martin)和欣革(Synge)最早提出塔板理論,將色譜柱比作蒸餾塔,把一根連續的色譜柱構想成由許多小段組成。在每一小段內,一部分空間為固定相占據,另一部分空間充滿流動相。組分隨流動相進入色譜柱後,就在兩相間進行分配。並假定在每一小段內組分可以很快地在兩相中達到分配平衡,這樣一個小段稱作一個理論塔板(theoretical plate),一個理論塔板的長度稱為理論塔板高度(theoretical plate height)H。經過多次分配平衡,分配係數小的組分,先離開蒸餾塔,分配係數大的組分後離開蒸餾塔。由於色譜柱內的塔板數相當多,因此即使組分分配係數只有微小差異,仍然可以獲得好的分離效果。

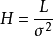
塔板理論是基於熱力學近似的理論,在真實的色譜柱中並不存在一片片相互隔離的塔板,也不能完全滿足塔板理論的前提假設。如塔板理論認為物質組分能夠迅速在流動相和固定相之間建立平衡,還認為物質組分在沿色譜柱前進時沒有徑向擴散,這些都是不符合色譜柱實際情況的,因此塔板理論雖然能很好地解釋色譜峰的峰型、峰高,客觀地評價色譜柱地柱效,卻不能很好地解釋與動力學過程相關的一些現象,如色譜峰峰型的變形、理論塔板數與流動相流速的關係等。
內容
塔板理論是色譜學的基礎理論,塔板理論將色譜柱看作一個分餾塔,待分離組分在分餾塔的塔板間移動,在每一個塔板內組分分子在固定相和流動相之間形成平衡,隨著流動相的流動,組分分子不斷從一個塔板移動到下一個塔板,並不斷形成新的平衡。一個色譜柱的塔板數越多,則其分離效果就越好。
基本假設
1) 色譜柱記憶體在許多塔板,組分在塔板間隔(即塔板高度)內完全服從分配定律,並很快達到分配平衡。
2) 樣品加在第0號塔板上,樣品沿色譜柱軸方向的擴散可以忽略。
3) 流動相在色譜柱內間歇式流動,每次進入一個塔板體積。
4) 在所有塔板上分配係數相等,與組分的量無關。
雖然以上假設與實際色譜過程不符,如色譜過程是一個動態過程,很難達到分配平衡;組分沿色譜柱軸方向的擴散是不可避免的。但是塔板理論導出了色譜流出曲線方程,成功地解釋了流出曲線的形狀、濃度極大點的位置,能夠評價色譜柱柱效。
2.色譜流出曲線方程及定量參數(峰高h和峰面積A)
由色譜流出曲線方程可知:當t=tR時,濃度C有極大值。Cmax就是色譜峰的峰高。因此:①當實驗條件一定時(即σ一定),峰高h與組分的量C0(進樣量)成正比,所以正常峰的峰高可用於定量分析。②當進樣量一定時,σ越小(柱效越高),峰高越高,因此提高柱效能提高HPLC分析的靈敏度。
由流出曲線方程對V(0~∞)求積分,即得出色譜峰面積A。可見A相當於組分進樣量C0,因此是常用的定量參數。把Cmax=h和Wh/2=2.355σ代入上式,即得A=1.064×Wh/2×h,此為正常峰的峰面積計算公式。
結論與意義
塔板理論導出了色譜流出曲線方程,成功地描述色譜流出曲線的位置和形狀,解釋組分的分離,提m定量評價柱效的參數,因此具有重要的理論和實際意義——例如,理論塔板數和理論塔板高度的概念和計算方法一直沿用,但塔板理論昕依據的分配平衡在色譜過程中只是一種理想狀態,它的某些假設與實際色譜過程並不相符,如要求組分立即達到分配平衡、流動相脈衝式進入色譜柱、忽略組分在色譜柱內的縱向擴散等。事實上,組分在兩相間分配需要一定時間、流動相連續進入色譜柱、組分在色譜柱中的縱向擴散也是不能忽略的。塔板理論沒有考慮各種動力學因素對色譜柱內傳質過程的影響,流出曲線方程不能說明載氣流速、固定相性質等凶素對色譜峰展寬的影響。