埃爾德什－莫德爾不等式

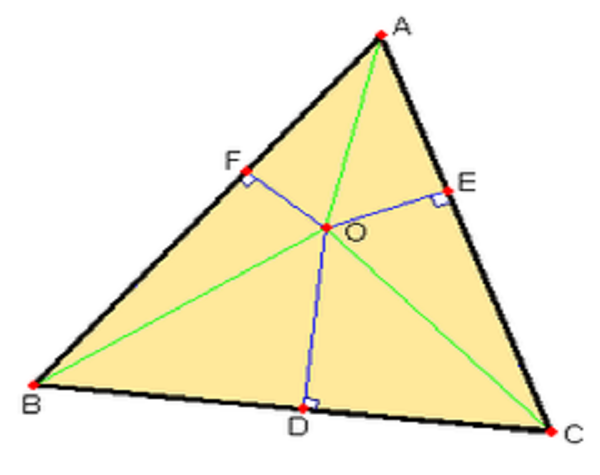
在幾何學中，埃爾德什-莫德爾不等式是一個二十世紀初期發現的不等式。埃爾德什-莫德爾不等式說明了：對於任何三角形ABC和其內部的一點O，點O到三角形三條邊的距離之和總是小於或等於點O到三角形的三個頂點的距離之和的一半。

埃爾德什-莫德爾不等式可以認為是幾何學中的歐拉定理的一個推廣。歐拉定理聲稱三角形外接圓的半徑總是大於等於內切圓半徑的兩倍。

基本介紹

• 中文名：埃爾德什－莫德爾不等式
• 外文名：Erdős–Mordell inequality
• 學科：數學

歷史

該不等式最早由埃爾德什在1935年在《美國數學月刊》上提出，作為第3740號問題。兩年之後，由路易斯·莫德爾和D.F.巴羅證明。1957年，卡扎里諾夫提出了一個更簡捷的證明。之後不斷有更簡潔、更基本的證明出現。1958年班考夫（Bankoff）給出了運用正交投影和相似三角形的證明，1997年和2004年出現了使用面積不等式的證明，1993年和2001年發現了根據托勒密定理的證明。

證明一

如圖1，O為三角形ABC中的一個點。O到三角形三邊的垂線分別交三條邊於D、E、F。設線段OA、OB、OC的長度分別是x、y、z，線段OD、OE、OF的長度分別是p、q、r，那么埃爾德什-莫德爾不等式為：

一個初等的證明方式是使用三角函式以及均值不等式。

首先，由於OF垂直於AF，OE垂直於AE，A、F、O、E四點共圓且OA為直徑，因此線段（角A為頂點A對應的內角）。

圖1

過點F、E作關於BC的垂線交BC於X、Y。過O作BC的平行線分別交FX、EY於U、V。由於OF垂直於AF，OE垂直於AE， ， 。於是：

另一方面，注意到在直角梯形中 中，斜腰EF的長度大於等於直角腰UV。因此：

類似地，還有：

三式相加，得到：

根據均值不等式， ，等等，於是最終得到：

這就是埃爾德什-莫德爾不等式。

從證明中可以看到，等號取得的充要條件是 ，也就是說不等式中的等號成立若且唯若三角形是等邊三角形。

證明二

這種方法能得到比埃爾德什-莫德爾不等式的結論更強的不等式。埃爾德什-莫德爾不等式僅僅是給出了點O到三角形3個頂點的距離OA、OB、OC與到3條邊的距離OD、OE、OF之間的關係，但以下不等式可以給出OA、OB、OC與OX、OY、OZ（其中OX、OY、OZ是3個小三角形的角平分線）之間的關係。

圖2，由於OD≤OX，OE≤OY，OF≤OZ，如果能夠證明：OA+OB+OC≥2(OX+OY+OZ)，就能直接得到我們想要的結論。

圖2

為了標記方便，設OA=a，OB=b，OC=c，OX=x，OY=y，OZ=z，∠BOC=2α，∠COA=2β，∠AOB=2γ。

在△BOC中，OX是角平分線。由角平分線長公式以及均值不等式，

同理有 。

要證明 ，只需要

以作為參變數，將上式整理得

這是一個開口向上的拋物線，要使得該式子成立，只需要判別式非正，即：

稍加整理，得

注意到

於是只要證明

該不等式明顯成立，因此原不等式成立。

需要特別注意的是，第一次我們用到了均值不等式，此時等號成立的條件為a=b=c，即O到三個頂點距離相等（即O是外心）。第二次我們用到了平方非負的性質，此時等號成立的條件是。由於α、β、γ的位置是平等的，所以結合兩個取等條件，可以得到，若且唯若O是外心且∠AOB=∠BOC=∠COA。又因為相等的圓心角所對的弦相等，因此可以得到此時△ABC是等邊三角形，並且OA=OB=OC，三線重合，此時的OX、OY、OZ恰好與OD、OE、OF重合。即埃爾德什-莫德爾不等式取等條件是△ABC為等邊三角形且O是等邊三角形的中心。