地面基準導航數據是以地球或指定的局部地面為基準的坐標系所表示的導航數據。
大地坐標系是一種與地球固連的地球參考系,分為全球坐標系和局部坐標系。全球坐標系的原點與地球質心(簡稱地心)重合,又稱地心坐標系;而局部坐標系的原點偏離地心可達數十米甚至數百米。
基本介紹
- 中文名:地面基準導航數據
- 外文名:ground-referenced navigation data
- 學科:航空航天
- 套用:導航
- 坐標系:以地球或指定的局部地面為基準
- 類型:導航數據
定義,大地坐標系統,其他坐標系,一種局部參考坐標系,
定義
地面基準導航數據是以地球或指定的局部地面為基準的坐標系所表示的導航數據。
大地坐標系統
大地坐標系統和高程系統是一個國家最基木、最重要的兩個大地測量基準,對於經濟建設、國防建設和經濟社會發展具有重要意義。大地坐標系統是地理坐標之參考基準,高程系統是海拔高之參考基準。大地坐標系統由坐標軸系和一參考橢球定義,由一批地麵點的高精度坐標和速度體現;高程系統則由高程零面和一批高程控制點的高程體現。
大地坐標系是一種與地球固連的地球參考系,分為全球坐標系和局部坐標系。全球坐標系的原點與地球質心(簡稱地心)重合,又稱地心坐標系;而局部坐標系的原點偏離地心可達數十米甚至數百米。以往受到測量技術限制,人們不得不採用局部坐標系。進入空間時代以來,地心坐標系興起並迅速發展,己被許多國家或地區所採用。
新中國成立初期,中國採用了1954年北京坐標系,20世紀90年代又啟用了1980西安坐標系。這2個坐標系都是採用常規測量技術建立的局部坐標系,現己不能適應經濟社會發展的需要,正逐漸退出歷史舞台。經國務院批准,從2008年7月起,中國啟用了新一代國家大地坐標系—2000中國大地坐標系(China Geodetic Coordinate System 2000, CGCS 2000)。它是一個地心坐標系,其定義和採用的參考橢球符合國際標準,其實現具體表現為大約2500個GNSS大地點(其中包括25個連續運行站)再參考曆元2000.0的坐標和速度,坐標精度為厘米級,速度精度一般好於3mm/年。
由一批地麵點坐標和速度實現了的坐標系稱為參考架。參考架不僅用來維持坐標系,也使坐標系便於使用。為維持坐標系,並使其保持必要的位置服務能力,CGCS 2000的參考架,從長遠來看,應由數以萬計的高精度空間測量站組成;從近期來看,應至少包括2500個GNSS連續運行站(大約平均每縣1個)和部分定期複測站,這些站還應進行水準和重力聯測。值得一提的是,一些省市目前己建不少GNSS連續運行站.若部分站給以改造利用,將有助於加強CGCS 2000的參考架。
其他坐標系
(1)機體坐標系(簡稱b系,xyz軸)一一機體坐標系與載體固連,原點在載體的重心,氣軸指向載體的縱軸方向,Z軸指向載體的豎軸方向,X軸指向載體的右側。機體坐標系相對地理坐標系的方位為載體的姿態角。
(2)計算坐標系(簡稱c系,xyz軸)一一慣導系統利用自身計算的載體位置來描述導航坐標系時,坐標系因慣導系統有位置誤差而產生誤差,這種坐標系稱為計算坐標系。它是計算機認為的當地地理坐標系,和真實的當地地理坐標系有小角度的誤差,一般在描述慣導誤差和推導慣導誤差方程時有用。
(3)平台坐標系(簡稱p系,xyz軸)一一原點在載體的重心,它是根據測量和計算需要,用慣性系統模擬的一種基準坐標系。在平台式指北慣導系統中,它指的是平台指向的坐標系,與平台固連,模擬的是地理坐標系。在捷聯式慣導系統中,它指的是“數學平台”,通過存儲在計算機中的姿態矩陣實現。平台坐標系是用來模擬導航坐標系的,如果平台無誤差,指向正確,則這樣的平台坐標系稱為理想平台坐標系。
(4)導航坐標系(簡稱n系,xyz軸)一一導航坐標系是慣導系統在求解導航參數時所採用的坐標系。通常,它與系統所在的位置有關。對平台式慣導系統而言理想的平台坐標系就是導航坐標系。例如,指北系統的平台理想指向為地理坐標系,此時,地理坐標系也是指北系統的導航坐標系。對捷聯慣導系統來說,導航參數並不在載體坐標系中求解,它必須將加速度計信號分解到某個求解導航參數較為方便的坐標系(對於指北系統來說就是地理坐標系)內,再進行導航計算,此坐標系就是導航坐標系。
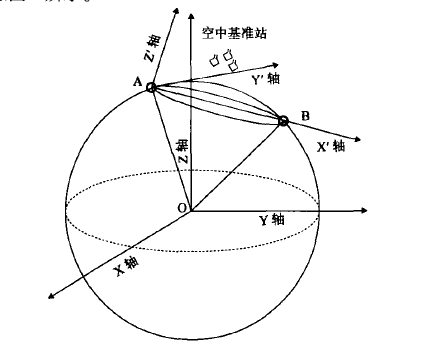
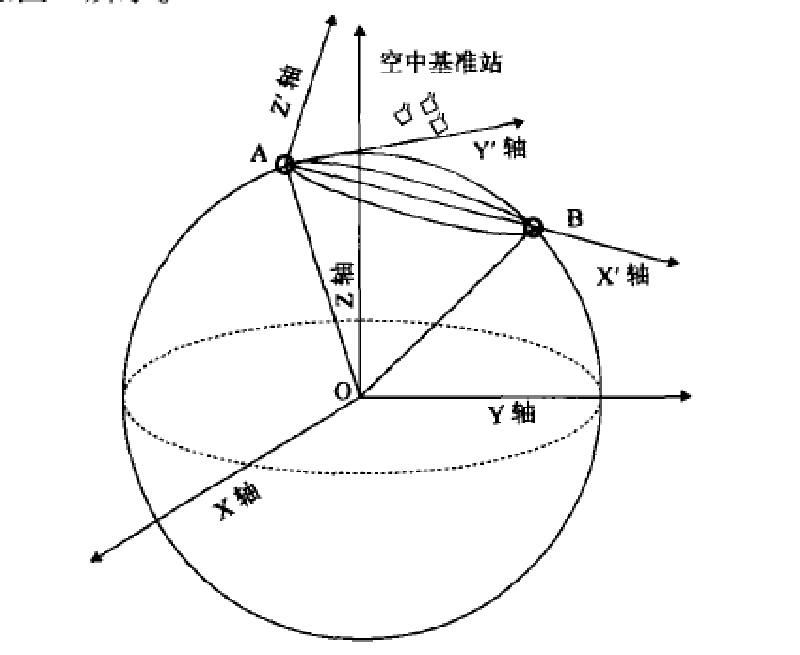
一種局部參考坐標系
無源時差定位具有精度高、可實時定位、適用性強等優點,有著廣泛的套用。
對空間目標,無源時差定位一般需要四個基準站,通過求解時差方程所構成的非線性方程組可以獲得目標輻射源的坐標。對位於地球表面的目標,由於可引入地球模型方程,則只需要3個基準站就可以完成定位。一般的求解方法是在地心坐標系下,利用WGS-84地球模型,聯立時差方程求解。這是一個非線性方程組,常採用牛頓疊代算法,通過線性化疊代進行定位解的數值計算;疊代初始點則通過簡化地球模型為球體,聯立時差方程,並求解一次四次方程得到。
但根據牛頓疊代算法的收斂定理,疊代初始點應位於真實點附近,否則容易造成疊代結果發散。但經典算法中求解初始點需要解一個四次方程,而四次方程的求解通常較為繁瑣,在實際套用中,當存在時差測量誤差時,增加了求解及判斷的計算量,有時無法判斷或者無解。
曾芳玲等提出一種基於局部參考坐標系下的定位算法,該方法通過坐標變換、近似處理和疊代運算,降低了目標點在三維直角坐標系下未知坐標的維數,從而可按照一般三個基準站計算二維坐標的定位算法完成對目標點的定位,求解與判斷較為容易,易於去除增根,從而保證計算結果。仿真結果顯示,經疊代運算後,該方法近似處理的影響較小,定位精度可滿足套用需求。