地貌形態示量圖是表示地表形態量度及其相互關係的地圖。地表形態特徵的各種現象,都存在量的對比關係,其中包括絕對高度、相對高度、寬度、長度、坡度、切割程度、切割密度等。
基本介紹
- 中文名:地貌形態示量圖
- 外文名:morphometric map
- 分類:地圖
- 性質:表示地表形態量度及其相互關係
- 內容:絕對高度、相對高度、寬度等
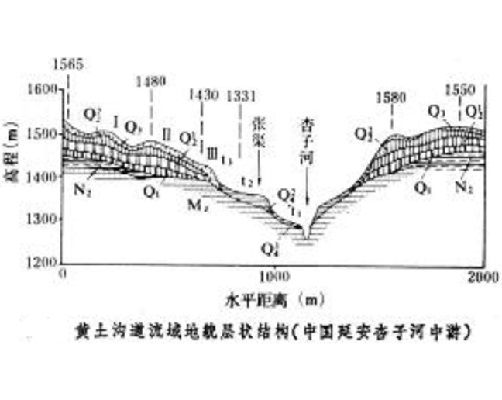
地貌形態示量圖是表示地表形態量度及其相互關係的地圖。地表形態特徵的各種現象,都存在量的對比關係,其中包括絕對高度、相對高度、寬度、長度、坡度、切割程度、切割密度等。
地貌形態示量圖是表示地表形態量度及其相互關係的地圖。地表形態特徵的各種現象,都存在量的對比關係,其中包括絕對高度、相對高度、寬度、長度、坡度、切割程度、切割...
地貌圖(geomorphic map)是專題性地圖,表示各種不同地貌標誌的地圖。反映各種不同地貌的外部形態特徵及成因、年代、發展過程、發育程度以及相互關係。可分為專門地貌圖...
地貌分類和地貌圖圖例系統,地貌圖製圖規範的研究歷史及現狀也做了詳細論述,並對黃土、沙漠、喀斯特、冰川等幾種特殊地貌及形態示量製圖問題,以及電子地貌圖系統的...
圖上應全面反映調查區內各種地貌類型的實際分布狀況和典型微地貌單元。 對研究平原城市最為重要的基礎圖件是地面坡度及坡地形態示量圖,地勢起伏程度圖、地表組成物質...
地貌圖例是測制地貌圖時描繪地貌對象所使用的各種圖形符號。地貌圖例必須建立在合理的地貌分類基礎上,主要建立在地貌 基本成因類型分類的基礎上。使用圖例時,作形態...
地貌是地圖要表示的基本要素之一,指由於地球內外應力的作用以及人類改造自然等因素,使地球表面呈現高低起伏的形態,如山地、丘陵、平原、高原、凹地、沖溝、陡崖等。...
地貌剖面圖系地貌研究的重要圖件之一。即:按一定比例尺記錄和揭示各種地貌外部形態和內部結構相互關係的切面圖件。地貌剖面圖可以根據各種地質地貌實際資料或檔案、...
在大比例尺地形圖上表示困難的內容(例如冰緣地貌等),沒有收入《圖集》《圖集》討論的重點內容是地貌形態特點及其高等線圖形特徵;第二、儘可能全面反映我國基本地貌...
起伏量圖又稱地勢圖,是表示地形在一定面積內相對高差的分布圖,以起伏量等值線表示之。中文名 起伏量圖 外文名 relief map 學科 地貌學 又稱 地勢圖 ...
地貌判讀是指利用軍用地形圖識別地貌特徵,並判斷其利用價值的工作。其內容包括地貌形態和地麵點的高程、高差及地面坡度的判定,通常需利用大於1:10萬比例尺地形圖...
地形地貌(topography),是指地勢高低起伏的變化,即地表的形態。分為:高原、山地、平原、丘陵、盆地五大基本地形(地貌形態)。 假如以圖形表示,也就是用等高線繪製出來...
地貌的形態在地圖上主要是用等高線顯示的 (二)等高線顯示地貌的特點 等高線顯示地貌有很多的特點:同一條線上各點的高度相等,並各自閉合;等高線多,山就高,等高線...
地勢圖上的等高線一般要密於同比例尺的其它普通地圖,反映地形特徵常採用不同的輔助等高線,且經常採用適當的地貌符號加強某些重要的微地貌形態和特種地貌形態的表示。...
實驗地形學也稱實驗地貌學,研究在實驗窒條件下模擬地貌形成過程。目的是揭示任何地貌形態的發生、發展和不同因素對地貌形成的影響,以及用數學方法表示地貌發育規律的...
地圖整飾主要包括:地圖符號設計,色彩設計,地貌立體表示,出版原圖繪製,圖面配置和...表示地面的起伏形態)、暈點法(以點的密度表示地面的起伏形態)、暈渲法(又叫...
