地球的模型和半徑
由於地球的自轉、內部密度的不均勻以及外部的潮汐力使得地球的形狀偏離球形。同時局部的地勢增大了這種不均勻性,使得地球的表面狀況極度複雜。為了便於處理,對地球表面的描述必須比實際更加簡單。因此我們建立一個能夠滿足需要的地球表面的最簡模型。
所有這些常用的模型都會涉及到“半徑”的概念。嚴格地說,立體圖形中只有球體才有半徑的概念,但在很多領域,包括處理地球的模型,都會擴展“半徑”的用法。以下是按照精確度降序的地球模型:
對於大地水準面和橢球體來說,模型上任何一點到指定中心的確定距離被稱為“地球的一條半徑”或“在某點地球的半徑”。同時也常用球體模型的“平均半徑”來作為“地球半徑”。另一方面,對應地球真實表面的“半徑”是沒有實際用處的。相反,相對於海平面的海拔才是有實際用途的。
地球的任何一條半徑長度都落在最小的約為6,357km的極半徑以及最大的約為6,378km的赤道半徑之間。因此地球形狀與標準球體的偏差只有約三百分之一,這在大多數情況下可以充分地把地球看做球體並使用術語“地球半徑”。這個概念也可以推廣到其他主要的行星上去,只不過扁率有差異而已。
地球變形的物理學
行星的旋轉使得其呈現“橢球形”:在赤道上凸起而在
極點平坦。所以赤道半徑a比極半徑b大約aq,其中扁率q等於:
測定方法
方法一
我們知道,地球的形狀近似一個球形,那么怎樣測出它的半徑呢?據說公元前三世紀時希臘天文學家
厄拉多塞內斯(Eratosthenes,公元前276—前194)首次測出了地球的半徑。

他發現夏至這一天,當太陽直射到賽伊城(今埃及亞斯文城)的水井S時,在亞歷山大城的一點A的天頂與太陽的夾角為7.2°(天頂就是鉛垂線向上無限延長與天空“天球”相交的一點)。他認為這兩地在同一條子午線上,從而這兩地間的弧所對的圓心角SOA就是7.2°(如圖1)。又知商隊旅行時測得A、S間的距離約為5000古希臘里,他按照弧長與圓心角的關係,算出了地球的半徑約為40000古希臘里。一般認為1古希臘里約為158.5米,那么他測得地球的半徑約為6340公里。
其原理為:
設圓周長為C,半徑為R,兩地間的的弧長為L,對應的圓心角為n°。
因為360°的圓心角所對的弧長就是圓周長C=2πR,所以1°的圓心角所對弧長是2πR/360,即πR/180。於是半徑為的R的圓中,n°的圓心角所對的弧長L為:
l=n*πR/180 ∴R=180L/(nπ)
當L=5000古希臘里,n=7.2時,
R≈180*5000/(7.2*3.14)=40000 (古希臘里)
化為公里數為:(公里)
40000*158.5/1000=6340 (公里)
厄拉多塞內斯這種測地球的方法常稱為弧度測量法。用這種方法測量時,只要測出兩地間的弧長和圓心角,就可求出地球的半徑了。
方法二
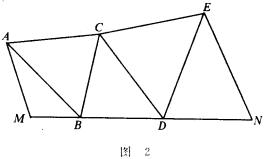
近代測量地球的半徑,還用弧度測量的方法,只是在求相距很遠的兩地間的距離時,採用了布設三角網的方法。比如求M、N兩地的距離時,可以像圖2那樣布設三角點,用經緯儀測量出△AMB,△ABC,△BCD,△CDE,△EDN的各個內角的度數,再量出M點附近的那條基線MA的長,最後即可算出MN的長度了。
通過這些三角形,怎樣算出MN的長度呢?這裡要用到三角形的一個很重要的定理——正弦定理。
即:在一個三角形中,各邊和它所對角的正弦的比相等。就是說,在△ABC中,有a/sinA =b/sinB =c/sinC。
在圖2中,由於各三角形的內角已測出,AM的長也量出,由正弦定理即可分別算出:
∴MN=MB+BD+DN。

如果M、N兩地在同一條子午線上,用天文方法測出各地的緯度後,即可算出子午線1°的長度。法國的皮卡爾(Pi-card.J.1620—1682)於1669—1671年率領他的測量隊首次測出了巴黎和亞眠之間的子午線的長,求得子午線1°的長約為111.28公里,這樣他推算出地球的半徑約為6376公里。(R≈111.28*180/3.1416≈6376(公里))
另外,布設三角網有多種方法,要根據實際情況,布設的網點越少越好。
隨著科學的發展,人們對地球的認識也越來越深入,並發現地球不完全是球形的,而是一個橢球體(如圖3)。科學家家們還找到了求得地球的長半徑a和短半徑b的方法,由於比較複雜,我們這裡就不介紹了,有興趣的同學可閱讀有關書籍。
半徑常用值
極半徑
從地心到北極或南極的距離,大約3950英里(6356.9088千米)(兩極的差極小,可以忽略)。
赤道半徑
是從地心到赤道的距離,大約3963英里(6377.830千米)。
平均半徑
大約3959英里(6371.393千米) 。這個數字是地心到地球表面所有各點距離的平均值。
可以這樣求:平均半徑=(赤道半徑×2+極半徑)/3
地球半徑有時被使用作為距離單位, 特別是在天文學和地質學中常用。它通常用
RE表示。
地球大概半徑6370.856千米。











