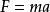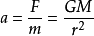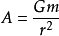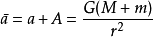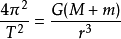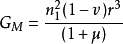地心引力常數GM是地球的基本特徵參數之一，單位為m3/s2。它是研究地球物理性質、地球重力場、地球動力形狀的重要參量；同時它在地球重力場範圍內及深空領域研究空間探測器及其運載工具的動態運動起著重要作用，它是空間探測器及其運載工具設計、遙測和遙控的重要參數；同時它在推導其他行星引力常數時也是重要的過渡參數。
基本介紹
- 中文名：地心引力常數
- 外文名：geocentric gravitational constant
- 時間：1964年
- 定義：萬有引力常數和地球總質量的乘積
介紹,觀測值,特點及原因,測定,
介紹
引力常數分為萬有引力常數、高斯引力常數和地心引力常數等，這些引力常數被套用於物理學、天文學和地球物理學的各種實驗測量中。萬有引力常數是牛頓萬有引力定律公式中的常數，一般用G表示；高斯引力常數用k表示，k2=G；地心引力常數用GM表示，單位為m3/s2，GM=G·M，M為地球質量。雖然它們的物理意義各不相同，但它們之間都有一定關係。按物理常數的定義，它們應是不變的，可是早在20世紀30年代前狄拉克就已提出萬有引力常數G隨時間而變化，以後好多學者都在理論上預測和實驗中觀測了G的變化值。此外，近年來，人們根據對人造衛星運動和飛向月球的火箭加速運動的觀測分析，指出地心引力常數也隨時間變化著。
觀測值
1964年召開的第12屆國際天文學協會通過的天文常數中，包括地心引力常數一項，當時採用的數值是GM=398603×109m3/s2。後來這個數值在1967年的國際測地和地球物理學協會上，列為“測地參考系統”的基本數據之一。從1968年起，世界各國都套用這個數字，計算天文年曆以及人造衛星和月球火箭等的運動。
地心引力常數隨時間的變化
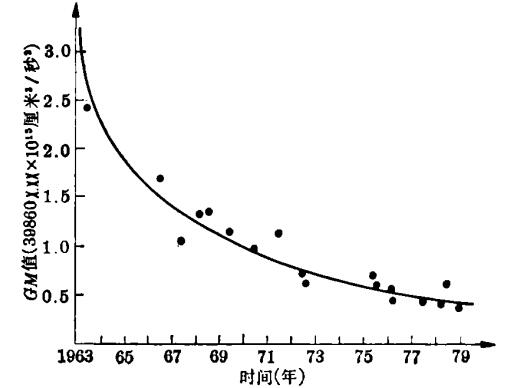地心引力常數隨時間的變化國際大地測量與地球物理聯合會第16屆大會地心引力常數的推薦值為（3986005±3）×108m3/s2（含大氣層）；國際大地測量與地球物理聯合會第17屆大會地心引力常數的推薦值為（39860047±5）×107m3/s2（含大氣層）；國際大地測量與地球物理聯合會第18屆大會地心引力常數的推薦值為（39860044±1）×107m3/s2（含大氣層）。
通過近十幾年來較為精確的測量，發現GM值有逐年下降的趨勢。為了得到表征這種變化的規律，利用1963~1979年由各種方法測得的、標準誤差小於0.8km3/s2的GM值進行最小二乘法擬合，其變化如圖。
特點及原因
近年來，通過對飛向月球的火箭加速運動的觀測分析，發現地心引力常數呈逐年下降趨勢。下表列出了國際天文協會（IAU）給出的一些年份的GM值。
| 年份 | GM/×109m3/s2 | 年份 | GM/×109m3/s2 |
|---|---|---|---|
1964 | 398603.00 | 1968 | 398601.15 |
1965 | 398602.20 | 1972 | 398600.80 |
1966 | 398601.30 | 1976 | 398600.50 |
1967 | 398601.22 | 1992 | 398600.44 |
由以上觀測數據可知，GM值的變化有以下2個特點：
（1）GM值呈逐年下降趨勢，如果令K=GM，則有：
，或
。
（2）GM值每年的下降值各不相同，即逐年下降值是不均勻的。
地心引力常數值變化的原因：地心引力常數值逐年下降的原因是由於萬有引力常數和地球質量兩者聯合變化的結果。
測定
地心引力常數的確定最好是用無線電測距法、雷射測量法、都卜勒法和射電干涉等方法對已發射的離地球甚遠的其它行星的空間探測器在其軌道的被動段測定，這樣可以使觀測更好地接近二體運動條件。如果利用地球人衛觀測方法確定地心引力常數，必須要足夠準確地顧及地球引力對衛星軌道的影響，特別是對衛星運動的平均角速度n和軌道長半軸a的影響。
從法方程的制約性來講，對橢園軌道的探測器是不利的。這時可改變觀測量為平均角速度n及軌道長半軸a的辦法來達到目的。
在利用雷射測月定位技術中，根據萬有引力定律可知，兩個質點之間是互相吸引的，這就是說，在地-月系統中，不僅地球吸引月球，使月球具有加速度a，同時月球也吸引地球，使地球具有加速度A。設地球質量M，月球質量m，由牛頓第二定律知
，所以月球加速
，同理，地球加速度
。
由於地球和月球各自受力方向相反，它們的加速度方向也相反，所以在相對運動中，月球相對地球的加速度：
；
又因作圓周運動的物體的向心加速度a=v2/r，將v=2πr/T代入，得
；
於是得行星運行周期同半徑的關係：
；
月球平均角速度n月=2π/T，由此可得地心引力常數計算公式：
；
式中ν為太陽等擾動影響改正項，μ=m/M為月球質量同地球質量比，r為月球軌道長半軸。
這是根據雷射測月原理來確定地心引力數的基本公式。根據雷射測月和其他研究資料的處理和分析，還可以大大地改進月球運動理論，更精確地確定μ值，並更可靠地確定月球雷射反射器的月面位置。雖然這種方法將受比例誤差的影響，但一般認為用這種方法確定的地心引力常數有較高的內部符合性。
