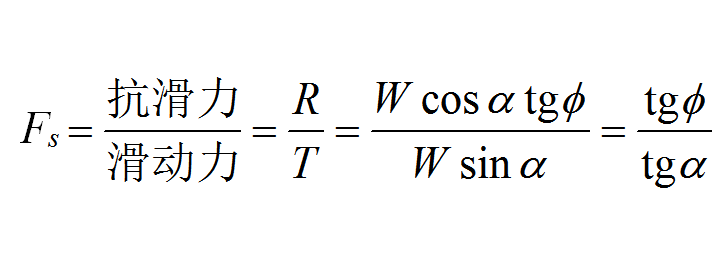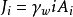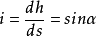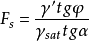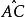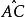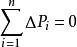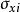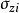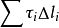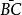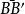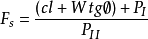土坡穩定分析是指根據滑裂土體的靜力平衡條件和強度理論，計算出沿該滑裂面滑動的可能性，即土坡穩定安全係數的大小或破壞機率的高低，然後，再系統地選取許多個可能的滑動面，用同樣的方法計算其穩定安全係數或破壞機率。
基本介紹
- 中文名：土坡穩定分析
- 外文名：slope stability analysis
- 學科：岩土工程
- 失穩原因：作用力發生變化等
- 分類：無粘性土坡、粘性土坡、天然土坡
- 方法：瑞典條分法等
簡介,土坡失穩原因,無粘性土坡穩定性分析,粘性土坡的穩定性分析,天然土坡的穩定問題,
簡介
在土木工程建築中，如果土坡失去穩定造成塌方，不僅影響工程進度，有時還會危及人的生命安全，造成工程失事和巨大的經濟損失。因此，土坡穩定問題在工程設計和施工中應引起足夠的重視。
天然的斜坡、填築的堤壩以及基坑放坡開挖等問題，都要演算斜坡的穩定性，亦既比較可能滑動面上的剪應力與抗剪強度。這種工作稱為穩定性分析。土坡穩定性分析是土力學中重要的穩定分析問題。土坡失穩的類型比較複雜，大多是土體的塑性破壞。而土體塑性破壞的分析方法有極限平衡法、極限分析法和有限元法等。在邊坡穩定性分析中，極限分析法和有限元法都還不夠成熟。因此，目前工程實踐中基本上都是採用極限平衡法。極限平衡方法分析的一般步驟是：假定斜坡破壞是沿著土體內某一確定的滑裂面滑動，根據滑裂土體的靜力平衡條件和莫爾—庫倫強度理論，可以計算出沿該滑裂面滑動的可能性，即土坡穩定安全係數的大小或破壞機率的高低，然後，再系統地選取許多個可能的滑動面，用同樣的方法計算其穩定安全係數或破壞機率。穩定安全係數最低或者破壞機率最高的滑動面就是可能性最大的滑動面。
土坡失穩原因
土坡就是由土體構成、具有傾斜坡面的土體，它的簡單外形如圖所示。一般而言，土坡有兩種類型。由自然地質作用所形成的土坡稱為天然土坡，如山坡、江河岸坡等；由人工開挖或回填而形成的土坡稱為人工土(邊)坡，如基坑、土壩、路堤等的邊坡。土坡在各種內力和外力的共同作用下，有可能產生剪下破壞和土體的移動。如果靠坡面處剪下破壞的面積很大，則將產生一部分土體相對於另一部分土體滑動的現象，稱為滑坡。土體的滑動一般系指土坡在一定範圍內整體地沿某一滑動面向下和向外移動而喪失其穩定性。除設計或施工不當可能導致土坡的失穩外，外界的不利因素影響也觸發和加劇了土坡的失穩，一般有以下幾種原因：
1．土坡所受的作用力發生變化：例如，由於在土坡頂部堆放材料或建造建築物而使坡頂受荷。或由於打樁振動，車輛行駛、爆破、地震等引起的振動而改變了土坡原來的平衡狀態；
2．土體抗剪強度的降低：例如，土體中含水量或超靜水壓力的增加；
3．靜水壓力的作用：例如，雨水或地面水流入土坡中的豎向裂縫，對土坡產生側向壓力，從而促進土坡產生滑動。因此，粘性土坡發生裂縫常常是土坡穩定性的不利因素，也是滑坡的預兆之一。
無粘性土坡穩定性分析
無粘性土坡即是由粗顆粒土所堆築的土坡。相對而言，無粘性土坡的穩定性分析比較簡單，可以分為下面二種情況進行討論。
一、均質的乾坡和水下坡均質的乾坡系指由一種土組成，完全在水位以上的無粘性土坡。水下土坡亦是由一種土組成，但完全在水位以下，沒有滲透水流作用的無粘性土坡。在上述二種情況下，只要土坡坡面上的土顆粒在重力作用下能夠保持穩定，那么，整個土坡就是穩定的。
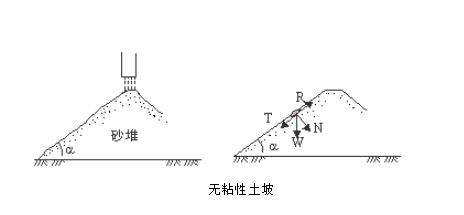
在無粘性土坡表面取一小塊土體來進行分析(右圖)，設該小塊土體的重量為W，其法向分力N=Wcos，切向分力T=Wsin。法向分力產生摩擦阻力，阻止土體下滑，稱為抗滑力，其值為R=N·tg=Wcos·tg。切向分力T是促使小土體下滑的滑動力。則土體的穩定安全係數Fs為：
式中：
φ——土的內摩擦角(°)；
α——土坡坡角(°)。
由上式可見，當α=φ時，Fs=1，即其抗滑力等於滑動力，土坡處於極限平衡狀態，此時的α就稱為天然休止角。當α<φ時，土坡就是穩定的。為了使土坡具有足夠的安全儲備，一般取Fs=1.1～1.5。
二、有滲透水流的均質土坡
當邊坡的內、外出現水位差時，例如基坑排水、坡外水位下降時，在擋水土堤內形成滲流場，如果浸潤線在下游坡面逸出，這時，在浸潤線以下，下游坡內的土體除了受到重力作用外，還受到由於水的滲流而產生的滲透力作用，因而使下游邊坡的穩定性降低。
滲流力可用繪流網的方法求得。作法是先繪製流網，求滑弧範圍內每一流網格線的平均水力梯度i，從而求得作用在格線上的滲透(流)力：
式中：
γw——水的重度；
Ai——格線的面積。
求出每一個格線上的滲透力Ji後，便可求得滑弧範圍內滲透力的合力TJ。將此力作為滑弧範圍內的外力(滑動力)進行計算，在滑動力矩中增加一項：
式中：lJ——TJ距圓心的距離。
如果水流方向與水平面呈夾角θ，則沿水流方向的滲透力j=γwi。在坡面上取土體V中的土骨架為隔離體，其有效的重量為γ'V。分析這塊土骨架的穩定性，作用在土骨架上的滲透力為J=jV=γwiV。因此，沿坡面的全部滑動力，包括重力和滲透力為：
T=γ’Vsinα+γwiVcos（α-θ）
坡面的正壓力為：
N=γ’Vcosα+γwiVsin（α-θ）
則土體沿坡面滑動的穩定安全係數：
式中：
i——滲透坡降；
γ‘——土的浮重度；
γw——水的重度；
φ——土的內摩擦角。
若水流在逸出段順著坡面流動，即θ=α。這時，流經路途ds的水頭損失為dh，所以，有
將其代入穩定安全係數公式，得：
由此可見，當逸出段為順坡滲流時，土坡穩定安全係數降低γ’/γsat。因此，要保持同樣的安全度，有滲流逸出時的坡角比沒有滲流逸出時要平緩得多。為了使土坡的設計既經濟又合理，在實際工程中，一般要在下游壩址處設定排水稜體，使滲透水流不直接從下游坡面逸出(右圖)。這時的下游坡面雖然沒有浸潤線逸出，但是，在下游坡內，浸潤線以下的土體仍然受到滲透力的作用。這種滲透力是一種滑動力，它將降低從浸潤線以下通過的滑動面的穩定性。這時深層滑動面(如圖中虛線表示)的穩定性可能比下游坡面的穩定性差，即危險的滑動面向深層發展。這種情況下，除了要按前述方法驗算坡面的穩定性外，還應該用圓弧滑動法驗算深層滑動的可能性。
粘性土坡的穩定性分析
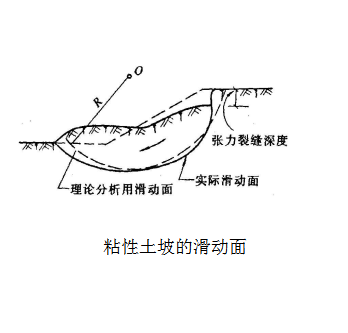
一般而言，粘性土坡由於剪下而破壞的滑動面大多數為一曲面，一般在破壞前坡頂先有張裂縫發生，繼而沿某一曲線產生整體滑動。圖7-5中的實線表示一粘性土坡滑動面的曲面，在理論分析時可以近似地將其假設為圓弧，如圖中虛線表示。為了簡化計算，在粘性土坡的穩定性分析中，常假設滑動面為圓弧面。建立在這一假定上的穩定性分析方法稱為圓弧滑動法。這是極限平衡方法的一種常用分析方法。
一、整體圓弧滑動法
此式即為整體圓弧滑動法計算邊坡穩定安全係數的公式。注意，它只適用於φ=0的情況。若φ≠0，則抗滑力與滑動面上的法向力有關，其求解可參閱下面的條分法。
二、瑞典條分法
所謂瑞典條分法，就是將滑動土體豎直分成若干個土條，把土條看成是剛體，分別求出作用於各個土條上的力對圓心的滑動力矩和抗滑力矩，然後按上述公式求土坡的穩定安全係數。
把滑動土體分成若干個土條後，土條的兩個側面分別存在著條塊間的作用力(右圖)。作用在條塊i上的力，除了重力Wi外，條塊側面ac和bd上作用有法向力Pi、Pi+1，切向力Hi、Hi+1，法向力的作用點至滑動弧面的距離為hi、hi+1。滑弧段cd的長度li，其上作用著法向力Ni和切向力Ti，Ti包括粘聚阻力ci·li和摩擦阻力Ni·tgφi。考慮到條塊的寬度不大，Wi和Ni可以看成是作用於cd弧段的中點。在所有的作用力中，Pi、Hi在分析前一土條時已經出現，可視為已知量，因此，待定的未知量有Pi+1、Hi+1、hi+1、Ni和Ti5個。每個土條可以建立三個靜力平衡方程，即ΣFxi=0，ΣFzi=0和ΣMi=0和一個極限平衡方程Ti=（Ni·tgφi+ci·li）/ Fs。
如果把滑動土體分成n個條塊，則n個條塊之間的分界面就有(n-1)個。分界面上的未知量為3(n-1)，滑動面上的未知量為2n個，還有待求的安全係數Fs，未知量總個數為(5n-2)，可以建立的靜力平衡方程和極限平衡方程為4n個。待求未知量與方程數之差為(n-2)。而一般條分法中的n在10以上。因此，這是一個高次的超靜定問題。為使問題求解，必須進行簡化計算。瑞典條分法假定滑動面是一個圓弧面，並認為條塊間的作用力對土坡的整體穩定性影響不大，故而忽略不計。或者說，假定條塊兩側的作用力大小相等，方向相反且作用於同一直線上。圖中取條塊i進行分析，由於不考慮條塊間的作用力，根據徑向力的靜力平衡條件，有：
Ni=Wicosθi
根據滑動弧面上的極限平衡條件，有：
Ti=Tfi/Fs=(ci·li+Ni·tgφi)/ Fs
式中：
Tfi——條塊i在滑動面上的抗剪強度；
Fs——滑動圓弧的穩定安全係數。
另外，按照滑動土體的整體力矩平衡條件，外力對圓心力矩之和為零。在條塊的三個作用力中，法向力Ni通過圓心不產生力矩。重力Wi產生的滑動力矩為：
∑Wi·di=∑Wi·R·sinθi
瑞典條分法是忽略了土條塊之間力的相互影響的一種簡化計算方法，它只滿足於滑動土體整體的力矩平衡條件，卻不滿足土條塊之間的靜力平衡條件。這是它區別於後面將要講述的其它條分法的主要特點。由於該方法套用的時間很長，積累了豐富的工程經驗，一般得到的安全係數偏低，即誤差偏於安全，所以目前仍然是工程上常用的方法。
三、畢肖甫條分法
畢肖甫(A.N.Bishop)於1955年提出一個考慮條塊間側面力的土坡穩定性分析方法，稱為畢肖甫條分法。此法仍然是圓弧滑動條分法。
在右圖中，從圓弧滑動體內取出土條i進行分析。作用在條塊i上的力，除了重力Wi外，滑動面上有切向力Ti和法向力Ni，條塊的側面分別有法向力Pi、Pi+1和切向力Hi、Hi+1。假設土條處於靜力平衡狀態，根據豎向力的平衡條件，應有：
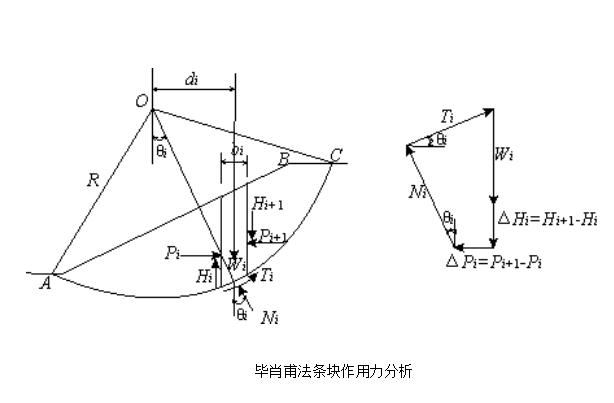
根據滿足土坡穩定安全係數Fs的極限平衡條件，有：
Ti =(ci·li+Ni·tgφi)/ Fs
與瑞典條分法相比，簡化的畢肖甫法是在不考慮條塊間切向力的前提下，滿足力的多邊形閉合條件，也就是說，隱含著條塊間有水平力的作用，雖然在公式中水平作用力並未出現。
所以它的特點是：(1)滿足整體力矩平衡條件；(2)滿足各個條塊力的多邊形閉合條件，但不滿足條塊的力矩平衡條件；(3)假設條塊間作用力只有法向力沒有切向力；(4)滿足極限平衡條件。由於考慮了條塊間水平力的作用，得到的穩定安全係數較瑞典條分法略高一些。很多工程計算表明，畢肖甫法與嚴格的極限平衡分析法，即滿足全部靜力平衡條件的方法(如下述的簡布法)相比，結果甚為接近。由於計算過程不很複雜，精度也比較高，所以，該方法是目前工程中很常用的一種方法。
四、普遍條分法(簡布法，N.Janbu)
普遍條分法的特點是假定條塊間水平作用力的位置。在這一假定前提下，每個土條塊都滿足全部的靜力平衡條件和極限平衡條件，滑動土體的整體力矩平衡條件也自然得到滿足。而且，它適用於任何滑動面，而不必規定滑動面是一個圓弧面，所以稱為普遍條分法。
它是由簡布提出的，又常稱為簡布法。
簡布公式如下：
比較畢肖甫公式和簡布公式，可以看出兩者很相似，但分母有差別，畢肖甫公式是根據滑動面為圓弧面，滑動土體滿足整體力矩平衡條件推導出的。簡布公式則是利用力的多邊形閉合和極限平衡條件，最後從
得出。顯然這些條件適用於任何形式的滑動面而不僅僅局限於圓弧面，在簡布公式中，ΔHi仍然是待定的未知量。畢肖甫沒有解出ΔHi，而讓ΔHi=0，從而成為簡化的畢肖甫公式。而簡布法則是利用條塊的力矩平衡條件，因而整個滑動土體的整體力矩平衡也自然得到滿足。
將作用在條塊上的力對條塊滑弧段中點Oi取矩(上圖(b))，並讓∑MOi=0。重力Wi和滑弧段上的力Ni和Ti均通過Oi，不產生力矩。
邊坡真正的穩定安全係數還要計算很多滑動面，進行比較，找出最危險的滑動面，其邊坡穩定安全係數才是真正的安全係數。這種計算工作量相當浩繁，一般要在計算機上計算。
五、有限元法
從瑞典條分法到普遍條分法的基本思路都是把滑動土體分成有限寬度的土條，把土條當成剛體，根據滑動土體的靜力平衡條件和極限平衡條件，求得滑動面上力的分布，從而可以計算出邊坡穩定安全係數Fs。但是，因為土體是變形體，而並非是剛體，所以，引用分析剛體的辦法來分析變形體，並不滿足變形協調條件，因而計算出的滑動面上的應力狀態不可能是真實的。有限元法就是把土坡當成變形體，按照土的變形特性，計算出土坡內的應力分布，然後，再把圓弧滑動面的概念引入其中，驗算滑動土體的整體抗滑穩定性。
將土坡劃分成許多單元體。用有限元法可以計算出每個土單元的應力、應變和每個結點的結點力和位移。這種計算目前已經成為土石壩應力變形分析的常用方法，有各種現成的程式可供套用。壩坡在重力的作用下剪下變形的軌跡類似於滑弧面。
土坡的應力計算出來以後，再引入圓弧滑動面的概念。把可能的圓弧滑動面劃分成若干個小弧段Δli，小弧段Δli上的應力用弧段中點的應力代表，其值可以按照有限元法應力分析的結果，根據弧段中點所在的單元的應力確定，表示為
，
，
。如果小弧段Δli與水平線的傾角為θi，則作用在弧段上的法向應力和剪應力分別為
將滑動面上所有小弧段的剪應力和抗剪強度分別求出來以後，再累加求得沿著滑動面總的剪下力
和抗剪力
。因此，邊坡穩定安全係數為：
很顯然，有限元分析方法的優點是把邊坡穩定分析與壩體的應力和變形分析結合起來。這時，滑動土體自然滿足靜力平衡條件而不必如條分法那樣引入人為的假定。但是，當邊坡接近失穩時，滑裂面通過的大部分土單元處於臨近破壞狀態，這時，用有限元法分析邊坡內的應力和變形所需要的土的基本特性，如變形特性，強度特性等均變得十分複雜，因此，要提出一種能反映土體實際受力狀況的計算模型是很不容易的。如果說在邊坡穩定性分析中極限平衡分析法是當前工程上主要套用的方法，那么，有限元方法則是一種潛在的具有很大發展前景的方法。
六、最危險滑裂面的確定方法和容許安全係數
（一）最危險滑裂面的位置
以上介紹的是計算某個位置已經確定的滑動面穩定安全係數的幾種方法。這一穩定安全係數並不代表邊坡的真正穩定性，因為邊坡的滑動面是任意選取的。假設邊坡的一個滑動面，就可計算其相應的安全係數。真正代表邊坡穩定程度的穩定安全係數應該是穩定安全係數中的最小值。相應於邊坡最小的穩定安全係數的滑動面稱為最危險滑動面，它才是土坡真正的滑動面。
確定土坡最危險滑動面圓心的位置和半徑大小是穩定分析中最繁瑣、工作量最大的工作。需要通過多次的計算才能完成。這方面費倫紐斯(W.Fellenius)提出的經驗方法，對於較快地確定土坡最危險的滑動面很有幫助。
費倫紐斯認為，對於均勻粘性土坡，其最危險的滑動面一般通過坡趾。在φ=0法的邊坡穩定分析中，最危險滑弧圓心的位置可以由右圖(a)中和夾角的交點確定。β1、β2的值與坡角α大小的關係，可由下表查用。
對於φ>0的土坡，最危險滑動面的圓心位置如圖(b)所示。首先按圖(b)中所示的方法確定DE線。自E點向DE延線上取圓心O1、O2…，通過坡趾A分別作圓弧，AC1、AC2、…，並求出相應的邊坡穩定安全係數Fs1、Fs2…。
坡角α | 坡度1∶m | β1 | β2 |
60° | 1∶0.58 | 29° | 40° |
45° | 1∶1.0 | 28° | 37° |
33°41′ | 1∶1.5 | 26° | 35° |
26°34′ | 1∶2.0 | 25° | 35° |
18°26′ | 1∶3.0 | 26° | 35° |
14°02′ | 1∶4.0 | 25° | 36° |
11°19′ | 1∶5.0 | 25° | 39° |
然後，再用適當的比例尺標在相應的圓心點上，並且連線成安全係數Fs隨圓心位置的變化曲線。曲線的最低點即為圓心在DE線上時安全係數的最小值。但是真正的最危險滑弧圓心並不一定在DE線上。通過這個最低點，引DE的垂直線FG。在FG線上，在DE延線的最小值前後再定幾個圓心O1'，O2'…，用類似步驟確定FG線上對應於最小安全係數的圓心，這個圓心。才被認為是通過坡趾滑出時的最危險滑動圓弧的中心。
當地基土層性質比填土軟弱，或者壩坡不是單一的土坡，或者壩體填土種類不同、強度互異時，最危險的滑動面就不一定從坡趾滑出。這時尋找最危險滑動面位置就更為繁瑣。實際上，對於非均質的、邊界條件較為複雜的土坡，用上述方法尋找最危險滑動面的位置將是十分困難的。隨著計算機技術的發展和普及，目前可以採用最最佳化方法，通過隨機搜尋，尋找最危險的滑動面的位置。國內已有這方面的程式可供使用。
（二）邊坡容許安全係數
在土坡穩定的分析中，從土體材料的強度指標到計算方法，很多因素都無法準確確定。因此，如果計算得到的土坡穩定安全係數等於1或稍大於1，並不表示邊坡的穩定性能得到可靠的保證。安全係數必須滿足一個最起碼的要求，稱為容許安全係數。容許安全係數值是以過去的工程經驗為依據並以各種規範的形式確定。因此採用不同的抗剪強度試驗方法和不同的穩定分析方法所得到的安全係數差別甚大，所以在套用規範所給定的土坡穩定容許安全係數時，一定要注意它所規定的試驗方法和計算方法。
運用條件 | 工程等級 | |||
Ⅰ | Ⅱ | Ⅲ | Ⅳ、Ⅴ | |
正常運用條件 | 1.3 | 1.25 | 1.2 | 1.15 |
非常運用條件Ⅰ | 1.2 | 1.15 | 1.1 | 1.05 |
非常運用條件Ⅱ | 1.1 | 1.05 | 1.05 | 1 |
註：正常運用條件系指：
（1）水庫水位處於正常高水位(或設計洪水位)與死水位之間的各種水位下的穩定滲流期；
（2）水庫水位在上述範圍內的經常性正常降落；
（3）抽水蓄能電站的水庫水位的經常性變化和降落。
非常運用條件Ⅰ系指：
（1）施工期；
（2）校核洪水位下有可能形成穩定滲流的情況；
（3）水庫水位的非常降落，如自校核洪水位降落、降落至死水位以下、大流量快速泄空等；
（4）正常運用條件遭遇地震。
非常運用條件Ⅱ系指以上非常運用條件(1)—(3)再遭遇地震的情況。
上表為1984年水電部頒布的《碾壓土石壩設計規範》(SDJ218—84)中的邊坡容許安全係數表。表中除註明者外，均適用於瑞典圓弧法。對Ⅰ、Ⅱ級的中、高土石壩以及一些複雜的情況，應同時採用畢肖甫法或其它更嚴格的方法(如普遍條分法等)進行計算。此時安全係數的容許值，應比表中所規定的值略微提高10%左右。對於Ⅰ級土石壩在正常使用條件下，安全係數不得小於1.5。
天然土坡的穩定問題
天然土體由於形成的自然環境、沉積時間以及應力歷史等因素不同，性質比人工填土要複雜得多，邊坡穩定分析仍然可按上述方法進行，但在強度指標的選擇上要更為慎重。
一、裂隙硬粘土的邊坡穩定性
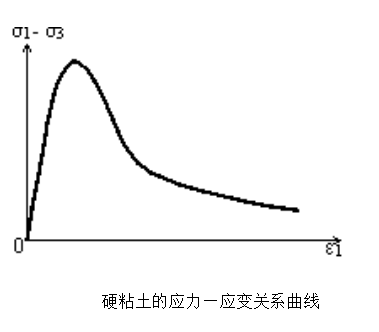
硬粘土通常為超固結土，其應力—應變關係曲線屬應變軟化型曲線，如圖所示。這類土如果也按一般的天然土坡穩定分析辦法，認為剪下過程中密度不變，故宜採用不固結不排水強度指標。用φu=0法計算，得到的穩定安全係數一般過大，造成偏於不安全的結果。下表是5個已發生滑坡的這類土的天然土坡或挖方的穩定性分析實例。表中數據表明，用φu=0法分析時，穩定安全係數均很大，但實際上都發生了不穩定破壞。其原因是土坡內滑動面上的剪應力分布不均勻，各點不能同時達到破壞。破壞過程是在某些部位土的剪應力首先達到峰值，而其它部位的土尚未破壞，於是隨著應變的不斷加大，已經破壞部位的強度不斷減小，直至變成殘餘強度。其它點也會相繼發生這種情況，形成所謂漸進性的破壞現象。在這種情況下，邊坡破壞的時間持續很長，而滑裂面的強度降至很低。有些天然滑坡體以及斷層帶，在其歷史年代上發生過多次的滑移，經受很大的應變，土的強度下降很多。在這種情況下驗算其穩定性時需注意選取其殘餘強度。
邊 坡 類 型 | 粘 土 資 料 | 安全係數 | 備 注 | ||||
W | WL | Wp | IP | （W-WP）/IP | |||
挖 方 | 24 | 57 | 27 | 30 | -0.10 | 3.2 | |
天然土坡 | 20 | 45 | 20 | 25 | 4.0 | 超固結 | |
挖 方 | 30 | 86 | 30 | 56 | 4.0 | 裂隙硬粘土 | |
挖 方 | 30 | 81 | 28 | 33 | 3.8 | ||
天然土坡 | 28 | 110 | 20 | 90 | 0.09 | 6.3 | |
二、軟土地基上土坡的穩定性分析
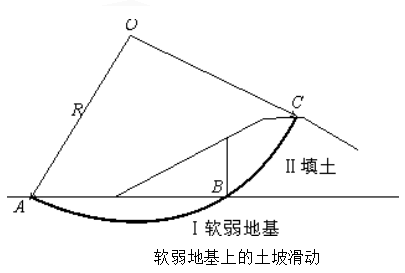
在軟弱地基上修築堤壩或路基，其破壞常由地基不穩定所引起。當軟土比較均勻，且厚度較大時，實地勘測和試驗表明其滑動面是一個近似的圓柱面，切入地基一定深度如圖中ABC所示。AB部分通過地基，BC部分通過壩體。根據瑞典圓弧法公式，Fs=MR/Ms。抗滑力矩MR由兩部分組成：一是AB段上抗滑力所產生的抗滑力矩MR I；另一部分是BC段上抗滑力所產生的抗滑力矩MRⅡ。考慮到軟土地基上的堤壩破壞時，在形成滑動面之前壩體一般已發生嚴重裂縫，或者軟土地基已經破壞而壩體部分的抗剪強度尚未完全發揮。因此，如果全部計算MRⅠ和MRⅡ，求得的穩定係數偏大。為安全起見，工程中有時建議對高度在5—6m以下的堤防或路堤，可以不考慮壩體部分的抗滑力矩。即讓MRⅡ=0，以此進行穩定分析(滑動力矩則應包括壩體部分的MsⅡ，而且是最主要的部分)。而對於中等高度的堤壩，則可考慮採用部分的MRⅡ，可根據具體工程情況並參照當地經驗，採用適當的折減係數，例如用0.5。
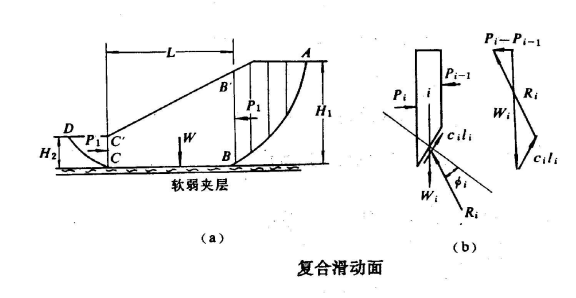
對於壩基內深度不大處有軟弱夾層時，滑動面將不是連續的圓弧面而是由兩段不同的圓弧和一段沿軟弱夾層的直線所組成的複合滑動面ABCD(右圖)。在這種情況下，土坡的穩定性分析可採用如下的近似方法計算。右圖中滑動土體由不同圓心和半徑的兩段圓弧AB和CD以及軟弱夾層面
組成。
用豎直線
和
將滑動土體分成ABB′、B'BCC'和C'CD三部分。第Ⅰ部分對中間第Ⅱ部分作用以推力PⅠ，第Ⅲ部分對中間第Ⅱ部分提供以抗力PⅡ。現在來分析中間部分土體B′BCC′的抗滑穩定性。其穩定安全係數可表達為：
式中：c、
——為軟弱夾層土的抗剪強度指標；
W——土體B′BCC′的重量；
l——滑動面在軟弱夾層上的長度；
PⅠ——土體ABB′作用於土體B′BCC′的滑動力，假定為水平方向；
PⅡ——土體CC′D對土體B′BCC′所提供的抗力，假定為水平方向。
PⅠ和PⅡ是兩個待定的力，可以用作圖法求之。
最後值得一提的是，無論是天然土坡還是人工土坡，在許多情況下,土體內都存在著孔隙水壓力。例如, 土體內水的滲流所引起的滲透壓力或者因填土而引起的超靜孔隙水壓力。孔隙水壓力的大小在有些情況下比較容易確定，而在有些情況下則較難確定或無法確定。例如穩定滲流引起的滲透壓力一般可以根據流網比較準確地確定，而在施工期、水位驟降期以及地震時產生的孔隙水壓力就比較難以確定。另外，土坡在滑動過程中的孔隙水壓力變化目前幾乎還沒有辦法確定。所以，在前面所討論的邊坡穩定計算方法中，作用於滑動土體上的力是用總應力表示，還是用有效應力表示，是一個十分重要的問題。顯而易見，用有效應力表示要優於用總應力表示。但是，鑒於孔隙水壓力不容易確定，故而有效應力法在工程中的套用尚存在實際困難。因此，這方面的工作還有待於進一步研究。
