類型
廣義的圖像運算是對圖像進行的處理操作,按涉及的波段,圖像運算可分為:①單波段運算;②多波段運算。按運算所涉及的像元範圍,圖像運算可分為:①點運算;②鄰域運算或局部運算;③幾何運算;④全局運算等。按計算方法與像元位置的關係可分為:①位置不變運算;②位置可變或位移可變運算。按運算執行的順序,又可分為①順序運算;②疊代運算;③跟蹤運算等。狹義圖像運算專指圖像的代數運算(或算術運算)、邏輯運算和數學形態學運算。
點運算
點運算是指:輸出圖像每個像素的灰度值僅僅取決於輸入圖像中相對應像素的灰度值。也就是說,點運算只涉及到一幅原圖像(稱為輸入圖像),運算對象是輸入圖像像素的灰度值。這種運算具有兩個特點:其一,根據某種預先設定的規則,將輸入圖像各個像素本身的灰度(和該像素鄰域內其他像素的灰度無關)逐一轉換成輸出圖像重對應像素的灰度值:其二,點運算不會改變像素的空間位置。因此,點運算也被稱為灰度變換。
由於點運算的結果是改變了圖像像素的灰度值,因此,也就可能改變了整幅圖像的灰度統計分布。這種改變也一定會在圖像的灰度直方圖上反映出來。而在實際中,有時可採取逆向操作。例如,首先根據需要設計出輸出圖像的灰度直方圖,然後確定由輸入圖像灰度直方圖改變成輸出圖像灰度直方圖所必須遵循的映射關係,也即灰度轉換函式,最後,按此轉換函式對輸入圖像的每一像素逐一執行點運算(灰度變換)。
點運算是圖像處理中一項基本而又重要的操作,一般都用於根據特定的要求規劃圖像的顯示。
算術運算
算術運算是指對兩幅或兩幅以上的輸入圖像中對應像素的灰度值作加、減、乘或除等運算 後,將運算結果作為輸出圖像相應像素的灰度值。這種運算的特點在於:其―,輸出圖像像素的灰度僅取決於兩幅或兩幅以上的輸入圖像的對應像素灰度值,和點運算相似,算術運算結果和參與運算像素的鄰域內像素的灰度值無關;其二,算術運算不會改變像素的空間位置。
圖像的相加或相乘可使某些像素的灰度值超出圖像處理系統允許的灰度上限值,而圖像的相減可使某些像素灰度值變為負數。實際套用中應充分考慮這些因素,並採取某些限定來避免此類事情的發生。例如,可以預先設定,凡圖像相減使灰度值之差為負數時,一律以0(灰度範圍的下限)來代替;除數為0的灰度值改為1;等等。
算術運算在圖像處理中有許多實用性很強的套用。例如,對多幅圖像求平均(包含了圖像相 加的運算),可以有效地消除或減弱靜止圖像中隨機噪聲的影響。除此以外, 在分子成像中常常採用高靈敏度的螢光成像模式或核醫學成像模式獲取研究對象的功能影像,而採用高空間解析度的X-CT或MRI成像模式獲取研究對象的解剖影像,再套用圖像融合技術綜合兩種成像模式分別得到的信息。在圖像融合處理中就可能用到圖像相加運算。
用圖像相減可以檢測研究對象的運動狀態。間隔一定時間後,對研究對象進行連續攝取, 如果研究對象處於靜止狀態,則這幾幅圖像完全相同,其差為零;如果研究對象處於活動狀 態(不論是隨機運動還是規律性運動),則這幾幅圖像差不會為零。因此,圖像之差能反映研 究對象的運動狀態。
幾何運算
圖像的幾何運算是指引起圖像幾何形狀發生改變的變換。與點運符不同的是,幾何運算可以看成是像素在圖像內的移動過程.該移動過程可以改變圖像中物體對象之間的空間關係。雖然幾何運算可以不受任何限制.但是通常都需要做出一些限制以保持圖像的外觀順序。
邏輯運算
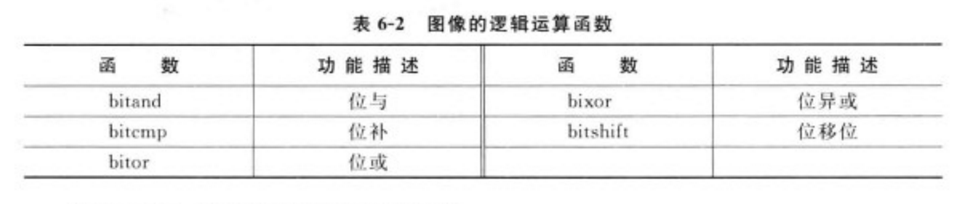
邏輯運算又稱為布爾運算。布爾用數學方法研究邏輯問題·成功地建立了邏輯運算.他用等式表示判斷,把推理看作等式的變換。這種變換的有效性不依賴人們對符號的解釋.只依賴於符號的組合規律。這一邏輯理論被稱為布爾代數。邏輯運算通常用來測試真假值。最常見到的邏輯運算就是循環的處理。用來判斷是否該離開循環或繼續執行循環內的命令。圖像的邏輯運算主要套用於圖像增強、圖像識別、圖像復原和區域分割等領域,與代數運算不同,邏輯運算既關注圖像像素點的數值變化.又重視位變換的情況.在MATLAB中,提供了一些邏輯運算函式,表6-2給出了這些圖像的邏輯運算函式.
套用
圖像運算是圖像處理中的常用處理方法,它以圖像為單位進行操作,運算的結果是一幅新的圖像,常常用於圖像高級處理(如圖像分割、目標的檢測和識別等)的前期處理。具體的圖像運算包括點運算、代數運算、幾何運算以及鄰域運算。代數運算常用於醫學圖像的處理以及圖像誤差檢測;幾何運算在圖像配準、校正等方面有重要用途;領域運算主要用在圖像濾波和形態學運算方面。
圖像的運算處理方法在許多領域得到突破性進展。下面舉兩例說明:
1、模式識別
尋找物體邊緣通常是通向物體自動識別的第一步.人眼和腦有非凡的識別能力,可以很好的從物體的粗略輪廓識別物體。要使計算機具有類似的能力,必須研究自動識別的算法並編成電腦程式。通常在邊緣檢測之後.因為邊緣檢測獲得的邊緣經常斷斷續續,邊緣像素過少,所以需要經過膨脹(dilation)和侵蝕(erosion)等步驟,幫助產生計算機可以辨明的物體邊界。
建立物體的清晰邊界之後,就可以考慮進行物體的鑑別、分類與識別了。在車站、機場 等處對行李進行透視檢測的設備就是從事此類工作的。利用目標物體集合中目標物的特徵由助於考察這個目標..比如計算物體的面積與周長、研究物體表面的紋理等。對物體進行識別通常將所分析的物體圖像與一系列可能存在的候選物進行特徵比對,如通過顏色和形狀來區分水果。可能存在的物體群越大,群中的物體越相似,所需要的特徵數目越大。利用統計方法依賴於給定物體出現於圖像中的一系列先驗槪率,其他一些方法則是用一系列訓 練圖像估計物體的特徵分布。另一種流行的模式識別技術是利用
神經網路(neural network)。
2、圖像頻譜與套用
圖像信號也具有頻譜,雖然它的頻譜比一般信號有更特別的解釋。一般來說,圖像頻譜 的低頻部分指那些灰度緩慢變化的部分,而高頻成份意味著快速變化,往往是圖像中物體的邊緣。
因為是從二維信號獲得的頻譜,所以包含著兩個方向的頻率數據。一個沿著圖像的行, 一個沿著圖像的列,因此,幅度和相位必須用第三維表示。一般在二維圖上用不同的顏色強度表示這些量大小,或在三維圖中用高度表示。二維DFT是首先沿圖像的行作一維DFT, 然後再沿中間結果數據的列作一維DFT。為提高計算速度,也存在2D FFT算法。一般要 確定一幅圖像需要圖像的幅度和相位兩部分信息,通過逆2D DFT變換即可精確還原圖像。 對於圖像頻譜,單獨的相位譜往往攜帶了建立圖像摹本的足夠信息,而幅度卻不能。


