圖像熵(image entropy)是圖像“繁忙”程度的估計值。
基本介紹
- 中文名:圖像熵
- 外文名:image entropy
- 定義:圖像“繁忙”程度的估計值
- 學科:計算機、熱力學等
- 領域:工程技術
定義,熵的特性,連續性,對稱性,極值性,可加性,進一步性質,信息熵,對比,參見,
定義
圖像熵表示為圖像灰度級集合的比特平均數,單位比特/像素,也描述了圖像信源的平均信息量。對於離散形式的二維圖像,其信息熵的計算公式為:

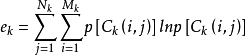
對於上式,其中,pi 為每一灰度級出現的機率。
熵指的是體系的混亂的程度,對焦良好的圖像的熵大於沒有清晰對焦的圖像,因此可以用熵作為一種對焦評價標準。熵越大,圖像越清晰。
圖像的熵是一種特徵的統計形式,它反映了圖像中平均信息量的多少,表示圖像灰度分布的聚集特徵,卻不能反映圖像灰度分布的空間特徵,為了表征這種空間特徵,可以在一維熵的基礎上引入能夠反映灰度分布空間特徵的特徵量來組成圖像的二維熵。
熵的特性
可以用很少的標準來描述熵的特性,將在下面列出。任何滿足這些假設的熵的定義均正比以下形式

其中,K是與選擇的度量單位相對應的一個正比常數。
下文中,pi= Pr(X=xi)且

連續性
該量度應連續,機率值小幅變化只能引起熵的微小變化。
對稱性
符號xi重新排序後,該量度應不變。
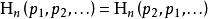
極值性
當所有符號有同等機會出現的情況下,熵達到最大值(所有可能的事件同等機率時不確定性最高)。

等機率事件的熵應隨符號的數量增加。

可加性
熵的量與該過程如何被劃分無關。
最後給出的這個函式關係刻畫了一個系統與其子系統的熵的關係。如果子系統之間的相互作用是已知的,則可以通過子系統的熵來計算一個系統的熵。
給定n個均勻分布元素的集合,分為k個箱(子系統),每個裡面有b1, ...,bk個元素,合起來的熵應等於系統的熵與各個箱子的熵的和,每個箱子的權重為在該箱中的機率。
對於正整數bi其中b1+ ... +bk=n來說,

選取k=n,b1= ... =bn= 1,這意味著確定符號的熵為零:Η1(1) = 0。這就是說可以用n進制熵來定義n個符號的信源符號集的效率。參見信息冗餘。
進一步性質
熵滿足以下性質,藉由將熵看成“在揭示隨機變數X的值後,從中得到的信息量(或消除的不確定性量)”,可來幫助理解其中一些性質。
增減一機率為零的事件不改變熵:

可用琴生不等式證明
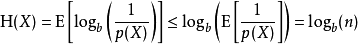
具有均勻機率分布的信源符號集可以有效地達到最大熵logb(n):所有可能的事件是等機率的時候,不確定性最大。
計算 (X,Y)得到的熵或信息量(即同時計算X和Y)等於通過進行兩個連續實驗得到的信息:先計算Y的值,然後在你知道Y的值條件下得出X的值。寫作
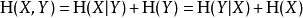
如果Y=f(X),其中f是確定性的,那么Η(f(X)|X) = 0。套用前一公式Η(X,f(X))就會產生

所以Η(f(X)) ≤ Η(X),因此當後者是通過確定性函式傳遞時,變數的熵只能降低。
如果X和Y是兩個獨立實驗,那么知道Y的值不影響我們對X值的認知(因為兩者獨立,所以互不影響):

兩個事件同時發生的熵不大於每個事件單獨發生的熵的總和,且僅當兩個事件是獨立的情況下相等。更具體地說,如果X和Y是同一機率空間的兩個隨機變數,而(X,Y)表示它們的笛卡爾積,則
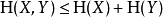
信息熵
在資訊理論中,熵(英語:entropy)是接收的每條訊息中包含的信息的平均量,又被稱為信息熵、信源熵、平均自信息量。這裡,“訊息”代表來自分布或數據流中的事件、樣本或特徵。(熵最好理解為不確定性的量度而不是確定性的量度,因為越隨機的信源的熵越大。)來自信源的另一個特徵是樣本的機率分布。這裡的想法是,比較不可能發生的事情,當它發生了,會提供更多的信息。由於一些其他的原因,把信息(熵)定義為機率分布的對數的相反數是有道理的。事件的機率分布和每個事件的信息量構成了一個隨機變數,這個隨機變數的均值(即期望)就是這個分布產生的信息量的平均值(即熵)。熵的單位通常為比特,但也用Sh、nat、Hart計量,取決於定義用到對數的底。
採用機率分布的對數作為信息的量度的原因是其可加性。例如,投擲一次硬幣提供了1 Sh的信息,而擲m次就為m位。更一般地,你需要用log2(n)位來表示一個可以取n個值的變數。
在1948年,克勞德·艾爾伍德·香農將熱力學的熵,引入到資訊理論,因此它又被稱為香農熵。
對比
信息熵的意義:信源的信息熵H是從整個信息源的統計特性來考慮的。它是從評價意義上來表徵信息源的總體特徵的。對於某特定的信息源,其信息熵只有一個。不同的信息源因統計特性不同,其熵也不同。
圖像的信息熵的意義:它表征圖像灰度分布的聚集特性,卻不能反映圖像灰度分布的空間特徵,為了表征這種空間特徵,可以在一維熵的基礎上引入能夠反映灰度分布空間特徵的特徵量來組成圖像的二維熵。
參見
- 熵 (生態學)
- 熵 (熱力學)

