割圓曲線(quadratrix)亦稱圓積線,一類特殊曲線,指解決化圓為方問題的曲線。求作一個正方形,使它的面積與已知圓的面積相等,稱為化圓為方問題。凡是可以用來解決化圓為方問題的曲線,都稱為割圓曲線。例如,阿基米德螺線、蝸牛線、琴豪生割圓曲線、奧扎南曲線都是割圓曲線。而最有名的要算狄諾斯特拉托斯割圓曲線y=x cot(πx/2a),(|x|≤a),狄諾斯特拉托斯割圓曲線是希皮亞斯(Hippias,(E))發現的,在各種曲線里,除去直線和圓以外,就算它發現得最早了,用它很容易解決三等分任意角問題,狄諾斯特拉托斯(Dinostratus)繼續研究這種曲線,發現可以用它解決化圓為方問題。
基本介紹
- 中文名:割圓曲線
- 外文名:quadratrix
- 別名:圓積線
- 發現者:希皮亞斯
- 套用:解三等分角和化圓為方問題
定義,割圓曲線的形成,化圓為方—求圓面積問題,利用割圓曲線解三等分角問題,
定義
割圓曲線是一種平面曲線,其直角坐標方程為 其中r 為以原點為圓心的圓的半徑(圖1,r=OA)。
其中r 為以原點為圓心的圓的半徑(圖1,r=OA)。

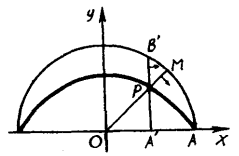 圖1
圖1割圓曲線亦可用動點的軌跡來定義。直線OM繞點O勻速轉動(順時針方向),與y軸平行的直線A'B'同時開始沿x軸方向平移。當OM旋轉90°時,A'B'恰好平移距離OA=r,這樣,OM與A'B'的交點P的軌跡就是割圓曲線之一段。
割圓曲線是在研究解古代三大作圖問題(化圓為方、三等分角和倍立方)時的一種數學成果。大約在公元前420年,希庇亞斯發現了稱做割圓曲線(quadratrix)的超越曲線,並發現它可以用於解三等分角和化圓為方兩個問題。
割圓曲線的形成
割圓曲線可由以下方法形成——
作一個正方形,它的底邊為AB,讓AB從底邊的位置開始沿反時針方向,以一個固定的角速度繞A點旋轉,另一方面,平行於AB的線段(其端點位於AD和BC)也從AB開始,以一個固定的線速度運動。這兩條運動線段的交點所形成的便是割圓曲線。以下的比總是相等的:

 圖2
圖2 圖3
圖3圖4說明了與割圓曲線上D,K和E相聯繫的一些點。水平的虛線段表示邊以固定的線速度運動,而沿圓弧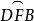 所引的半徑表示線段以固定的角速度運動。它們的交點D,I,J,K,L,M,E是割圓曲線上的點。
所引的半徑表示線段以固定的角速度運動。它們的交點D,I,J,K,L,M,E是割圓曲線上的點。
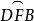
 圖4
圖4化圓為方—求圓面積問題
設ABCD 是正方形,BED 是圓的一個象限,圓心在點A。
設:(1)圓的半徑均勻地繞著A轉動,由AB轉到AD的位置;(2)同時,直線BC亦均勻地沿著BA與AD平行地移動,最後移到AD的位置。於是轉動的半徑和移動的直線最後都與AD重合,而在這以前,轉動的半徑和移動的直線將有交點,如F或N。這種點的軌跡稱為割圓曲線(quadratrix),圖5。
 圖5
圖5這曲線的性質是: ∠BAD :∠EAD= 弧BED :弧ED= AB :FH。
設割圓曲線與AD 交於G,如果能夠證明:
象限BED的弧長:AB= AB:AG。
那么就可求得象限BED的弧長,因而就可求得圓周的長度。設上述的比不等於AB:AG,不妨設這比等於AB:AK,AK或大於AG,或小於AG。
(1) 設AK>AG,圖6,以A 為圓心,AK 為半徑,作象限KFL 交割圓曲線於F,交AB於L。聯結AF,延長AF交圓周BED於E,作FH 垂直於AD。
 圖5
圖5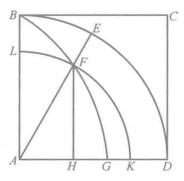 圖6
圖6根據假定
弧BED :AB= AB : AK= 弧BED : 弧LFK。
所以,AB= 弧LFK,
但由割圓曲線的性質:
AB : FH=弧BED :弧ED=弧LFK:弧FK。
已經證得AB=弧LFK,則得FH=弧FK,這是不可能的,因此AK 不能大於AG。
(2) 設AK<AG,以A為圓心,AK 為半徑,作象限KML,作AD的垂線KF交割圓曲線於F,聯結AF,交兩個象限於M,E(圖7)。
 圖7
圖7如前,可證得:
AB= 弧LMK。
由割圓曲線的性質有:
AB :FK= 弧BED:弧DE=弧LMK : 弧MK。
由AB= 弧LMK,得FK= 弧KM,這是不可能的,因此AK不能小於AG。
總之,AK=AG,即:象限BED的弧長: AB=AB : AG。
象限的弧長既可求得,那么圓周長亦可求得。根據阿幾米德書中的定理:圓的面積等於以圓周長為底、半徑為高的直角三角形的面積,就可求得圓的面積了。
這個方法是有問題的,問題在於怎樣確定點G? 有人說,可將象限BED 平分,即作AE,使∠DAE=45*,作B'C',則AB'= AB。再將∠DAE平分,得AE',二等分AB' 得B”,作B”C”,繼續下去,最後可得到在AD上的一點G,但這樣的方法乃是窮竭法,只能近似地得到G點,AG 的值是近似值,那么圓周長,圓面積都不可能是正確無誤的數值。其實,對化圓為方問題有興趣的不僅是希臘人,6 世紀的博埃斯(Boethius) 說,從亞里士多德時代以後,嘗試去解這問題的有許多人,博埃斯自己對用尺規作圖法去解此問題也是有過各種幻想的,許多人認為自己獲得解決了,但他們往往在無意中用進了不可能的或特殊條件的假設,然而也遇到了推翻自己論點的批評。直到1882 年林德曼(Lindemann)證明π的超越性以後,人們才完全認識到化圓為方問題是不可能用尺規作圖法去解決的。
AB。再將∠DAE平分,得AE',二等分AB' 得B”,作B”C”,繼續下去,最後可得到在AD上的一點G,但這樣的方法乃是窮竭法,只能近似地得到G點,AG 的值是近似值,那么圓周長,圓面積都不可能是正確無誤的數值。其實,對化圓為方問題有興趣的不僅是希臘人,6 世紀的博埃斯(Boethius) 說,從亞里士多德時代以後,嘗試去解這問題的有許多人,博埃斯自己對用尺規作圖法去解此問題也是有過各種幻想的,許多人認為自己獲得解決了,但他們往往在無意中用進了不可能的或特殊條件的假設,然而也遇到了推翻自己論點的批評。直到1882 年林德曼(Lindemann)證明π的超越性以後,人們才完全認識到化圓為方問題是不可能用尺規作圖法去解決的。

利用割圓曲線解三等分角問題
設已知角為∠DAX,置角頂A於圓心,在圓內作割圓曲線,設AX 交割圓曲線於F,交圓於E。作FH⊥AD,將FH 三等分於K,作KL//AD,KL交割圓曲線於L,那么∠DAL 就是∠DAX 的三等分角,圖8。
 圖8
圖8因由割圓曲線的性質:弧ED:弧MD= FH : KH,
因為KH=  FH,故:弧MD=
FH,故:弧MD= 弧ED,
弧ED,


因此∠LAD= ∠DAX。
∠DAX。

注意:如果將FHn等分,利用割圓曲線就可將已知角n等分。

