從n個不同元素中不重複地取出m(1≤m≤n)個元素在一個圓周上,叫做這n個不同元素的圓排列。如果一個m-圓排列旋轉可以得到另一個m-圓排列,則認為這兩個圓排列相同。
基本介紹
- 中文名:圓排列
- 範圍:數據結構的一種
定義
計算公式

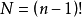
生成算法
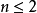


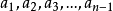
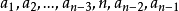
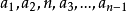
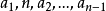
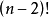
算法證明
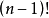
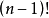
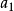

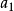
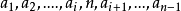
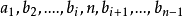
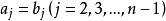
舉例
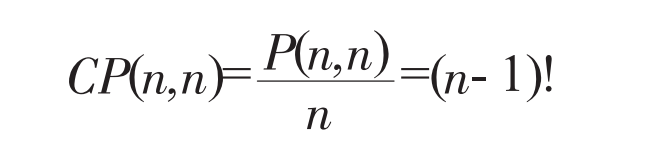
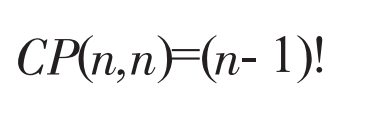

遞歸實現
#include <algorithm>#include <stdio.h>#include <cstdio>#include <cstring>#define MAX_NUM 32using namespace std;typedef uint32_t T;T p[MAX_NUM];int n;void init_p() { for (int i = 0; i < n; i++) p[i] = i + 1;}inline void swap_circle(int i, int j) { T tmp = p[i]; p[i] = p[j]; p[j] = tmp;}/*輸出*/inline void output(int start) { for(int i = 0 ; i < n ; i += 1) { printf("%d", p[(start + i) % n]); if(i != n-1) printf(" "); } printf("\n");}/* 圓排列生成 */void generate_circle(int len) { if (n <= 2) { output(0); return; } if (len == n) { T tmp[MAX_NUM]; memcpy(tmp, p, n * sizeof(T)); for (int i = 1; i < n; ++i) { output_circle(); swap_circle(n-i,n-i-1); } memcpy(p, tmp, n * sizeof(T)); return; } else { T tmp[MAX_NUM]; memcpy(tmp, p, n * sizeof(T)); for (int i = 0; i < len - 1; i++) { generate_circle(len + 1); swap_circle(len - 1 - i, len - 2 - i); } memcpy(p, tmp, n * sizeof(T)); }}int main(int argc, char * argv[]) { scanf("%d", &n); init_p(); //freopen("output.txt", "w",stdout); /*輸出到檔案*/ generate_circle(3); return 0;}