圓劈錐曲面(circular conoid)是一種特殊的劈錐曲面，指導向曲線是一個圓的劈錐曲面，圓劈錐曲面的導向曲線稱為導向圓。劈錐曲面是一種曲面，它是由一條平行於已知平面(方向平面)且和已知直線(方向直線)以及已知曲線(方向曲線)相交的直線運動而生成的，當方向曲線為平面曲線時，該方向曲線不得在方向平面上。劈錐曲面是直紋曲面。例如，正螺旋面就是一種劈錐曲面，其方向平面垂直於其軸線，方向曲線——螺旋線，而方向直線——旋轉軸。
基本介紹
- 中文名：圓劈錐曲面
- 外文名：circular conoid
- 所屬學科：數學
- 所屬問題：立體幾何(多面體)
- 簡介：導向曲線是一個圓的劈錐曲面
基本概念,其他介紹,圓劈錐曲面是直紋曲面,克卜勒法則計算體積,
基本概念
給定直線a，平面N內的曲線C，平面M，且a∥N，a和M相交，則滿足下述條件的動直線的軌跡稱為劈錐曲面(如圖1)：
1.動直線平行於平面M；
2.動直線與直線a，曲線C均相交；
其中，定直線a、定曲線C、定平面M分別稱為劈錐曲面的導向直線、導向曲線、導向平面，動直線稱為劈錐曲面的母線，劈錐曲面被導向直線分成的兩部分，稱為劈錐曲面的兩葉(圖1中只畫出劈錐曲面的一葉)；劈錐曲面的每一葉，稱為半劈錐曲面。
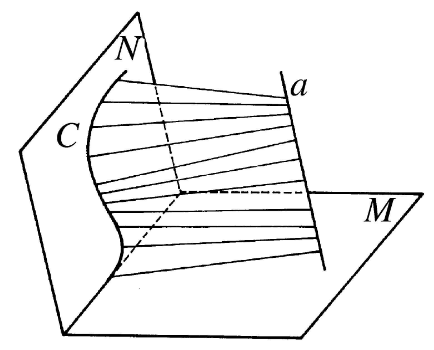
圖1
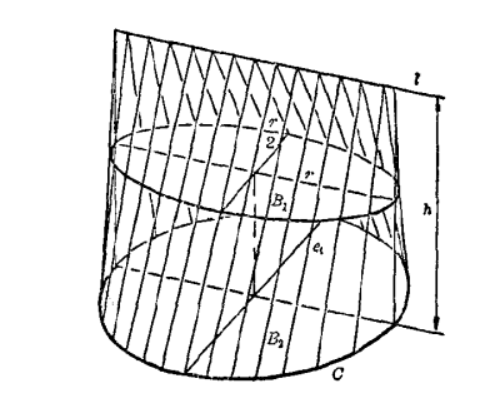
在技術套用中，劈錐曲面具有很重要的實用價值。一般說來，劈錐曲面可由如下方法得到。給定一導向曲線C，一導向直線l和一不平行於l的方向平面，平行於平面與C和l相交的直線集就構成了劈錐曲面。如果導向曲線是個圓，圓平面不包含導向直線，這就叫圓劈錐曲面。如果導向直線垂直於方向平面，且與圓平面外側的圓軸線相交成直角，這就叫直立正圓劈錐曲面。與圓平面平行的平面截圓劈錐曲面成一橢圓(圖2)。
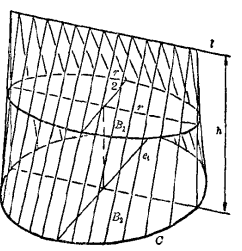
圖2
其他介紹
圓劈錐曲面是直紋曲面
直紋曲面 兩端在兩條各別的曲線上滑動的直線線段所形成的任何曲面稱為直紋曲面。當兩曲線是在空間的兩條相對傾斜直線時，直紋曲面就是雙曲拋物面(圖3)，雙曲拋物面具有位於曲面上的一對直線族。柱面是由在兩條相同的平行豎曲線上滑移一水平直線而形成的直紋曲面(圖4)。
在平行平面內的兩條不同的曲線上滑移一直線段，可形成一族不同的直紋曲面，這類曲面稱為截錐曲面。截錐曲面屋頂覆蓋矩形平面，且可以讓光線從給定方向(通常是從北面)進入室內(圖5)。
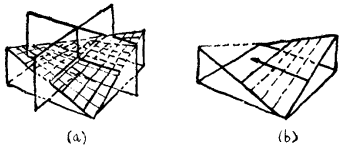
圖3
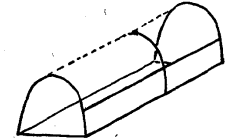
圖4
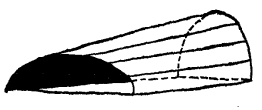
圖5
劈錐曲面 由一端在曲線上，另一端在一直線上滑移一直線段所形成的曲面稱為劈錐曲面(圖6)。劈錐曲面根據它的端曲線是圓弧、拋物線還是橢圓弧而分別稱為圓劈錐曲面、拋物線劈錐曲面或橢圓劈錐曲面。劈錐曲面是一種鞍形曲面，它的主曲率線說明在端曲線頂點到對角的連線方向的曲率是向上的，而另一主曲率是向下的(圖6)。劈錐曲面可用作以曲線端為固定端的懸臂殼，此時常使橫向曲率朝上(圖7)。
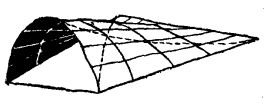
圖6
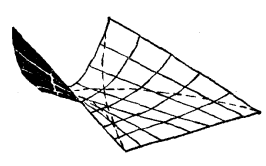
圖7
克卜勒法則計算體積
克卜勒(Kepler)法則 有些計算立體體積的近似公式在實際計算中非常有用，在很多特例中這些公式能給出準確值。
在關於琵琶桶立體幾何的一部巨著中，克卜勒(1571~1630年)給出了確定琵琶桶體積V的近似公式，式中B0, B2, B1是桶的頂和底面及中間截面的面積，h是琵琶桶的高。
克卜勒法則：
克卜勒法則運用於直立正圓劈錐曲面時（圖2），所得體積是準確的。如果用r表示底圓半徑，h表示高，則
