圈基(circuit basis)圖G的循環空間的一組基,循環空間的維數稱為圈秩或簡稱上秩。上循環空間的一組基稱為上圈基,上循環空間的維數稱為上圈秩或簡稱秩。
基本介紹
- 中文名:圈基
- 外文名:circuit basis
- 所屬學科:數學
- 所屬問題:圖論(循環空間)
- 相關概念:循環空間,點空間等
基本介紹









相關概念
點空間






生成樹

秩多項式




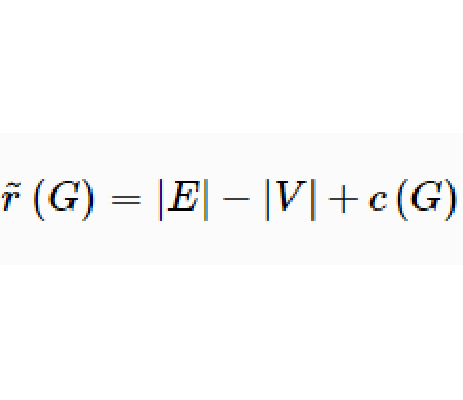
圈基(circuit basis)圖G的循環空間的一組基,循環空間的維數稱為圈秩或簡稱上秩。上循環空間的一組基稱為上圈基,上循環空間的維數稱為上圈秩或簡稱秩。




















圈基(circuit basis)圖G的循環空間的一組基,循環空間的維數稱為圈秩或簡稱上秩。上循環空間的一組基稱為上圈基,上循環空間的維數稱為上圈秩或簡稱秩。基本介紹 圈基是圖G的循環空間(參見下文“點空間”)的一組基,循環空間...
1 定義 2 相關性質 3 圈基 4 子圖多項式與秩多項式 定義 編輯 對於圖 ,記其中, 分別為以S為邊集的G的支撐子圖的秩和上秩(參見“圈基”),稱 為圖G的秩多項式 [1] 。相關性質 編輯 1...
胎圈底部 定義 胎圈底部}}ead has。又稱胎圈基部。指輪胎與輪輛胎l} 座接觸的部位。其作用是保持胎圈與輪惘底部相著合。
朋友圈點讚了撈到了嗎 點一個贊分享我的回憶 告訴你我所有的新經歷 朋友圈點讚了撈到了嗎 我說親你是消費不起的負擔 讓我矗立在你的黑名單中想你 我說親有一天離你而去 讓我消失在你的朋友圈 百度魔圖模糊了你的臉 找一種...
圈的讀音有juàn,quān,juān,又名“環”,古兵器。用金屬製成的圓環。圓環的直徑約為25厘米,環外緣大部有刃,並有一握手處。多用雙圈。常見的有乾坤日月圈、月牙圈、風火輪、雙環等。圈不易練習,屬雙器械,較重身法變化,在...
話題圈,是由深圳市騰訊計算機系統有限公司開發的一款社交類手機軟體,有iOS和安卓兩個版本,在各大套用市場均已上線。基本參數 大 小:19.7MB 支持系統:Android/iOS 收費形式:免費 行 業:社交 基本簡介 話題圈是一個以話題討論為...
成圈,在經編針織機上用織針和其他成圈機件使紗線形成線圈的過程。基本原理 與緯編針織成圈過程的編結法相似。在經編機上,平行排列的經紗從經軸上引出,分別墊放到各根織針上進行成圈。每根紗線一般每次只對一或二根織針墊紗,成...
數圈APP是廣東數圈科技有限公司於2019年11月推出的一款學習互動軟體,擁有分析測試,知識課堂,社群交流等內容。數圈APP將西方的《數字學》和東方的《易經》相結合,是一款專注為客戶提供解決實際問題的工具。基本介紹 數圈APP是一款為...
科庫電子科技 內容介紹 考托路漫漫,托福圈相伴 “托福圈”是一款集功能性與社交性於一體的托福備考神器。將實用的“聽說讀寫”等備考功能與便捷一體化的社交功能相融合,實力帶你備戰托福,全能化的質感體驗,讓你無壓力全方位備考。
私密圈是歡聚時代(YYInc)運營的一款匿名朋友圈移動社交套用。2014年初,美國的匿名社交軟體secret開始火爆,它從一個新奇的角度,引爆了人們的這種隱性需求。業內人士稱“秘密”爆紅的速度堪比微信。2014年5月14日,多玩發布“秘密圈”...
《法律圈》是2015年上線的一款手機軟體。基本信息 APP名稱:法律圈 更新:2014-05-02 版本:1.02 要求:Android 2.2以上、IOS8 功能:按照專業領域、地域劃分及定位系統對國內律師進行全面搜尋 依照效力級別、類別及地區劃分等方式獲悉...
